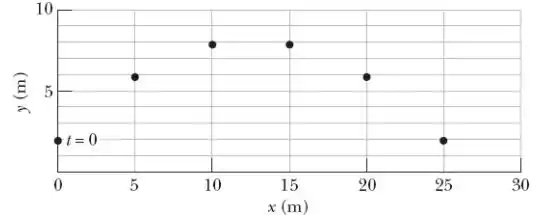
132- Uma competição de atletismo é realizada em um planeta de um sistema solar distante. Um arremessador de peso lança o peso de um ponto 2,0 m acima do nível do solo. Um gráfico estroboscópico da posição do peso aparece na Fig. 4-61, em que as leituras foram tomadas a cada 0,50 s e o peso foi arremessado no instante t = 0.

(a)Qual é a velocidade inicial do peso, em termos dos vetores unitários?

(b) Qual é o módulo da aceleração de queda livre no planeta?

(c) Quanto tempo após ter sido arremessado o peso toca o solo?

(d) Se um arremesso de peso for feito na Terra nas mesmas condições, quanto tempo após o lançamento o peso tocará o solo?

O que nos dá a necessidade de encontrar uma outra equação, uma vez que estamos em outro planeta e esse outro planeta, além de ter uma outra língua (provavelmente), também tem uma outra gravidade.

Para isso vamos utilizar outro ponto, como o primeiro que é . O que nos dá uma equação igual a:

O tempo que o peso leva para sair da origem até o primeiro ponto é de , o que nos dá uma equação de movimento igual a:

Substituindo a equação encontrada no passo nessa última equação nós teremos:

b) A gravidade desse planeta então será:

Logo será:

Logo a componente da velocidade em vetores unitários será:

c) O peso não toca o solo em como é o tempo que encontramos no passo 1, esse é o tempo que o peso chega no mesmo nível do seu ponto de lançamento. Encontrando então o tempo total de deslocamento temos:

Por Bháskara encontramos as seguintes raízes:

Como não podemos admitir tempos negativos então o tempo de queda desse peso é de:

d) Na terra a gravidade é de o que nos dá um tempo total igual a:

Uma vez que as velocidades iniciais não são alteradas.

Por Bhaskara temos as raízes iguais a:

Utilizando a raiz positiva temos que na terra o projétil tocaria o chão em: