Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 11.Problemas - Ex. 19
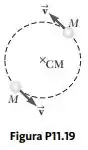
O sistema binário de Plaskett consiste em duas estrelas que giram numa órbita circular em torno de um centro de massa a meio caminho entre elas. Essa afirmação implica que as massas das duas estrelas são iguais (Fig. P11.19). Suponha que a velocidade orbital de cada estrela seja e o período orbital de cada uma, dias. Procure a massa de cada estrela. (Para comparação, a massa do nosso Sol é de .)
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Aplicando a segunda lei de Newton para cada estrela:
Podemos escrever r em termos do período, T, considerando o tempo e a distância de um ciclo completo. A distância percorrida em uma órbita é a circunferência da órbita comum das estrelas, então . Portanto,
Resposta
Exercícios de Livros Relacionados
Num ônibus espacial, em uma órbita de 300 km de altitude, precisa-se realizar uma experiência a uma distância considerável da nave. Para tanto, uma carga útil de 100 kg é “baixada” em direção à Terra
Estrelas grandes podem explodir depois que terminam de queimar seu combustível nuclear, causando o aparecimento de uma supernova. A explosão detona as camadas externas da estrela. De acordo com a terc
O Sistema Solar está a 25.000 anos-luz do centro da Via Láctea. Um ano-luz é a distância que a luz percorre em um ano a uma velocidade de 3,0 × 10 8 m/s. Astrônomos comprovaram que o Sistema Solar orb
Em 1996, o Observatório Solar e Heliosférico (SOHO) “estacionou” em uma órbita ligeiramente interior à órbita terrestre, conforme ilustra a FIGURA PD13.70. Nesta órbita, o período do satélite é de exa