Indutores e Indutância
Teoria
Introdução
Você lembra que nós estudamos que fluxos de campos magnéticos variando induzem uma força eletromotriz?
Mas será que é possível quantificar essa capacidade que um circuito tem de induzir ? Sim, é aí que entra a indutância.
Bora lá!
Indutores
Um dispositivo que é capaz de gerar variações de fluxo magnético em um circuito e como consequência disso induzir uma força eletromotriz é chamado de indutor.
Essa capacidade de induzir é o que chamamos de indutância.
O indutor é capaz de induzir em outros circuitos (indutância mútua) e em si mesmo (autoindutância)
Note que todo e qualquer circuito que passe uma corrente não-estacionária tem alguma espécie de indutância, pois com a corrente variando, o módulo do campo magnético também varia e com isso haverá uma variação do fluxo de campo, beleza?
Mas o único caso que vamos estudar aqui é o mais simples, que é o fio enrolado em espiral, ou seja, nosso querido solenóide.
Autoindutância
A autoindutância é um fenômeno que ocorre numa espira ou solenóide, e é proveniente do campo produzido pela sua própria corrente.
Se um solenóide com espiras conduz uma corrente , essa corrente vai produzir um fluxo magnético na região central do indutor.
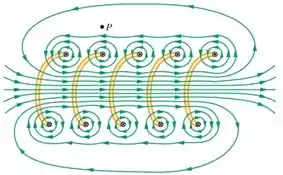
Agora você concorda comigo que se a corrente variar com o tempo, o fluxo induzido nessa região central também varia?
Pela Lei de Faraday:
Esta é batizada carinhosamente de auto induzida. O sentido dessa auto induzida é dado pela Lei de Lenz, se opondo à variação que a produz.
Como o fluxo total pelo circuito é vezes o fluxo em cada volta do fio, temos que:
Substituindo, podemos tirar a constante fora da derivada:
Que fluxo de campo magnético é esse? É o fluxo do campo gerado pela própria corrente no solenoide. Lembra como é a fórmula do campo gerado por um solenóide? É essa aqui!
(Se não lembra, dá uma olhada no nosso tópico de “Lei de Ampère em Solenóides e Toróides”)
Assim, se definirmos o vetor área do solenóide paralelo ao vetor campo magnético, o fluxo do campo magnético através do solenoide vai ser:
Onde é a área da seção transversal do solenoide.
Aí a fem induzida vai ser
Como todo esse cara multiplicando a derivada da corrente é constante, nós definimos ela como , a chamada autoindutância:
A unidade de medida da indutância é chamada henry e é definida por:
Então, a nossa autoindutância pode ser expressa de duas maneiras:
Ou
Solenóides Longos
Toda vez que o problema falar em “solenóide longo”, acaba sendo mais jogo, ao invés de calcularmos a autoindutância, calcularmos a autoindutância por unidade de comprimento, dada por:
Onde é a área transversal do indutor, e é o número de espiras por unidade de comprimento, dado por:
Indutância Mútua
A medida da tendência de um circuito induzir corrente num outro circuito é chamada de indutância mútua. Suponhamos que temos dois solenoides, só que, inicialmente, o circuito não tem corrente:
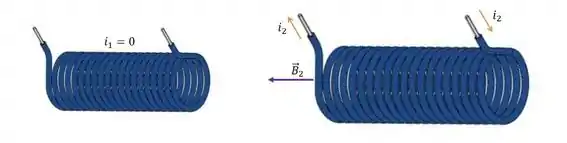
Sejam:
e : As correntes em cada solenóide, com ;
e : Número de espiras em cada solenóide;
e : Fluxo magnético por através de uma volta de cada solenoide;
e : Fem em cada solenoide.
Nós vamos ter que, pela Lei de Faraday:
Como o fluxo total pelo circuito é vezes o fluxo por cada volta do fio, temos:
Substituindo, podemos tirar a constante fora da derivada:
Até aqui nada de muito novo. A novidade vem da seguinte afirmativa: O fluxo no circuito é proporcional à corrente no circuito . Isso ocorre porque o fluxo de campo no circuito 1 é gerado pela corrente que passa no circuito 2.
Ou seja:
Quando duas coisas são proporcionais, existe uma constante de proporcionalidade que relaciona elas. Essa constante é a indutância mútua :
Dito isso, podemos derivar ambos os lados com respeito ao tempo:
Substituindo a expressão da Lei de Faraday:
Ou seja, a induzida no circuito é diretamente proporcional à variação de corrente no .
Até aqui beleza, a corrente no circuito induziu uma no circuito .
Agora o circuito tem uma nova corrente própria e, já que ele tem corrente, vai fazer um campo próprio:
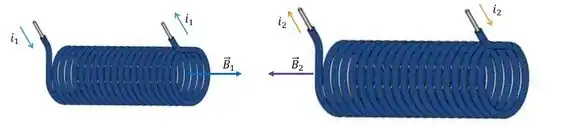
Se ele tem um campo próprio, olha que maravilha: ele vai induzir uma no circuito ! Virou doidera? Não, porque nós somos malandros.
O fio tinha uma fem própria antes , e agora ele vai ter essa antiga mais a induzida pelo fio . Mas nós só estamos preocupados em calcular a induzida, e ela pode ser encontrada pelo mesmo método que usamos para achar a do circuito . Sabemos que o fluxo induzido no é proporcional à corrente no :
E essa constante de proporcionalidade, não por acaso, é a indutância mútua entre os circuitos:
Derivando ambos os lados e substituindo a Lei de Faraday para o circuito :
Finalmente, podemos tirar que a definição da indução mútua é:
Quando formos analisar essas equações, temos que ter muito cuidado. Primeiramente, a indutância mútua é uma constante que depende apenas da geometria dos dois circuitos (número de espiras, comprimento, área da seção reta, etc.) e não da corrente ou do campo magnético.
Veja que temos várias maneiras de calcular a indutância mútua, depende só do que foi dado pela questão. Apesar de ser um conceito novo, temos todas as ferramentas para calcular o seu valor.
Tá, agora só mais uma coisinha...
Solenóides Preenchidos com Materiais Magnéticos
Em casos raros, alguns problemas colocam solenóides preenchidos por materiais magnéticos. Assim, é valido tocar no assunto.
No interior de um material magnético, o campo magnético será dado por:
Onde é o campo magnético no vácuo e é uma propriedade adimensional chamada suscetibilidade magnética.
Nesse caso, a autoindutância em um indutor preenchido por material magnético será:
Onde é a autoindutância no vácuo.
É isso! Bora lá exercitar?
Solenóides Longos
Indutância Mútua
Solenóides Preenchidos com Materiais Magnéticos
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 298-40.
A indutância de uma bobina compacta de espiras é . Calcule o fluxo magnético através da bobina quando a corrente é .
Passo 1
A indutância do indutor é definida por:
Logo, o fluxo magnético será:
Onde:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 298-44.
Um indutor de conduz uma corrente de . Qual deve ser a taxa de variação da corrente para que a força eletromotriz no indutor seja ?
Passo 1
A auto induzida é dada por:
Logo:
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 298-41.
Uma bobina circular tem de raio e espiras compactas. Um campo magnético externo de módulo é aplicado perpendicularmente ao plano da bobina.
Se a corrente na bobina é zero, qual é o fluxo magnético que enlaça as espiras?
Quando a corrente na bobina é em um certo sentido, o fluxo magnético através da bobina é zero. Qual é a indutância da bobina.
Passo 1
Se a corrente na bobina é zero, qual é o fluxo magnético que enlaça as espiras?
O fluxo magnético é definido por:
Onde .
Onde:
Portanto:
Passo 2
Quando a corrente na bobina é em um certo sentido, o fluxo magnético através da bobina é zero. Qual é a indutância da bobina.
A indutância e definida por:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 298-45.
Em um certo instante a corrente e a força eletromotriz auto-induzida em um indutor têm os sentidos indicados na figura abaixo.
A corrente está aumentando ou diminuindo?
A força eletromotriz induzida é e a taxa de variação da corrente é . Determine a indutância.
Passo 1
A corrente está aumentando ou diminuindo?
De acordo com a lei de Lenz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela quer dizer é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
Beleza!
Como a induzida é sempre do contra, quando a corrente está aumentando, a está no sentido contrário (atrapalhando), e quando a corrente está diminuindo, a está no mesmo sentido (ajudando).
Então, como a está no mesmo sentido da corrente, é como se ela estivesse “ajudando” a corrente. Logo, a corrente está diminuindo.
Passo 2
A força eletromotriz induzida é e a taxa de variação da corrente é . Determine a indutância.
Por definição, a indutância será dada por:
Onde:
Logo:
Resposta
A corrente está diminuindo.
Exercício Resolvido #5
UFRJ – Física III – Prova 2 – 2012.2 – Múltipla Escolha nº5.
Um solenoide circular ideal, muito longo, tem número de espiras , raio e comprimento . Se alterarmos o raio e o número de espiras de tal solenoide, para o dobro e a metade, respectivamente, mantendo seu comprimento inalterado, o que ocorre com a sua autoindutância? Considere que o solenoide é muito longo (“infinito”): .
- Aumenta
- Diminui
- Depende da corrente que passa no solenoide
- Não se altera
Passo 1
Conforme estudamos no capítulo, a autoindutância só depende da geometria do indutor e nunca da corrente que passa por ele. Conforme demonstramos em exercício de fixação (se você não viu a demonstração, sinta-se livre para decorar o resultado aqui abaixo) temos que a autoindutância de um solenoide é:
Proporcional ao quadrado do número de espiras;
Proporcional à área:
E inversamente proporcional ao comprimento:
Passo 2
O que ele quer dizer com o dado do “solenoide infinito” é que quando mudarmos o número de espiras isto não vai alterar o comprimento. Portanto esta última relação qualitativa não vai nos interessar. Das relações qualitativas observadas, podemos escrever a autoindutância como:
Onde é uma constante de proporcionalidade. Ela engloba o comprimento neste caso, pois o enunciado o supôs constante.
Passo 3
No enunciado ele dobra o raio. Como a área de seção reta é um círculo:
Passo 4
Ele também pega a metade do número de espiras:
Substituindo os novos valores do enunciado:
Ou seja, a autoindutância nova é igual à antiga.
Resposta
Letra d
Exercício Resolvido #6
UFRJ – Física III – Prova 2 – 2014.1 – Múltipla Escolha nº7.
Seja um solenoide longo, formado por um enrolamento de espiras circulares. Considere as seguintes três afirmativas sobre sua autoindutância: (I) ela é proporcional ao quadrado do raio das espiras; (II) ela é proporcional à taxa de variação da corrente no solenoide, e (III) ela é proporcional à corrente que circula no solenoide. Assinale a opção que indica qual(is) dessas afirmativas está(ão) correta(s).
- Nenhuma
- Apenas a I
- Apenas a II
- Apenas a III
- Apenas a I e a II
- Apenas a I e a III
- Apenas a II e a III
- Todas
Passo 1
Sabemos que a auto-indutância é proporcional a:
Ou seja, sim, é proporcional ao quadrado do raio das espiras pois .
Passo 2
Não à taxa de variação da corrente. Nada da corrente influi na indutância, ela é uma constante que depende da geometria do elemento de circuito.
E também não é proporcional à corrente que circula, pelo motivo supracitado.
Resposta
Letra b
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 300-72.
Dois solenóides fazem parte do circuito de ignição de um automóvel. Quando a corrente em um dos solenóides diminui de para zero em uma força eletromotriz de é induzida no outro solenóide.
Qual é a indutância mútua dos solenóides?
Passo 1
A induzida no segundo solenóide é dada por
Logo:
Como a corrente varia linearmente:
Logo:
Onde:
Finalmente:
Resposta
Exercício Resolvido #8
UFRJ – Física III – Prova 2 – 2014.2 – Múltipla Escolha nº1.
Considere um solenoide ideal de raio e uma espira circular de raio coaxial a ele, e suponha que (ou seja, a espira está fora do solenoide).
Pelo solenoide passa uma corrente não-estacionária . Denotando a indutância mútua do sistema por , as autoindutâncias do solenoide e da espira por e , e o campo produzido pelo solenoide em seu exterior por , qual das afirmações abaixo é verdadeira?
pois .
depende de .
pois .
depende de .
depende de .
depende de .
Passo 1
Bom, todas as opções trabalham com , ou , ou ... então vamos calcular cada um desses caras, beleza?
A indutância mútua desse sistema será dada por:
Como as áreas tanto solenoide, quando da espira, são constantes, os fluxos magnéticos vão depender somente dos campos magnéticos.
Logo:
Lembrando que, como o solenoide induz corrente na espira e vice-versa:
Se continuarmos as contas, eventualmente as corrente irão sumir da expressão de . Assim, das opções acima, vai depender de .
Logo, a resposta certa é a letra .
Mas, por via das dúvidas, vamos dar uma olhada nas autoindutâncias, ok?
Passo 2
A autoindutância do solenoide é dada por:
Como a área do solenoide é constante e o campo em seu interior é uniforme, podemos reescrever a expressão acima como:
Se lembrarmos que, para a autoindutância, , novamente, se continuarmos as contas vamos ver que a corrente vai sumir da expressão.
Como , logo, não depende de .
Passo 3
Seguindo o mesmo raciocínio para a autoindutância da espira, teremos:
Logo, não depende de .
Resposta
depende de .
Exercício Resolvido #9
UNICAMP – Física III – Prova 3 – 2012.1 – Manhã – Questão nº1.
Dois fios longos e paralelos, cada um de raio , cujos centros estão separados por uma distância , são percorridos por corrente iguais , mas de sentidos opostos, conforme a figura.
Calcule:
- O módulo, a direção e o sentido do campo magnético , no ponto , devido aos fios.
- O fluxo magnético através de um retângulo formado pelas linhas tracejadas e os dois lados externos dos fios. Considere um comprimento e despreze o fluxo dentro dos fios.
- A indutância para este par de fios.
Passo 1
- O módulo, a direção e o sentido do campo magnético , no ponto , devido aos fios.
O campo magnético gerado por um fio pode ser calculado facilmente através da lei de Ampère:
Nesse caso, a nossa curva é uma circunferência que de raio , que é a distância entre o fio e o ponto que queremos calcular o campo magnético.
Assim, o campo magnético é, resumindo a fórmula, igual a:
Vamos calcular o campo magnético de cada fio, separadamente.
- Fio da esquerda:
- Fio da direita:
Para este fio, a corrente interna será e ele se encontra a uma distância do ponto , logo:
Através da regra da mão direita, vemos que o campo magnético gerado por esse fio vai estar entrando na página.
Nesse fio passa a mesma corrente , mas ele está a uma distância do ponto . Portanto:
Novamente, pela regra da mão direita, o campo magnético gerado por esse fio estará entrando na página.
Como acabamos de ver, os dois fios geram campos magnéticos que “entram na página” no ponto . Portanto, o campo magnético resultante será:
Onde apontando para dentro da página.
Passo 2
Por definição, o fluxo magnético é dado por:
Podemos dizer que e, substituindo a expressão do campo magnético que encontramos no passo 1, teremos:
Como o problema nos disse para desprezar o fluxo dentro dos fios, vai variar entre e . Continuando...
Passo 3
Por definição, a indutância é dada por:
Esse par de fios funciona como uma espira única. Portanto, .
Resposta
a.
Apontando para dentro do plano da página.
b.
c.
Exercício Resolvido #10
USP – Física III – Prova 3 – 2015 – Questão nº2.
Um anel condutor de raio está no plano e centrado na origem de um sistema de coordenadas. Outro anel condutor , concêntrico a possui raio , conforme a figura.
Calcule a indutância mútua entra os dois anéis. Justifique as aproximações feitas.
No anel circula uma corrente . Calcule a força eletromotriz induzida no anel 1 pelo anel 2.
Dado: O campo magnético no centro de um anel de raio por onde passa uma corrente é .
Passo 1
Calcule a indutância mútua entra os dois anéis. Justifique as aproximações feitas.
Por definição, a indutância mútua é dada por:
Como , é razoável dizer que o campo magnético no interior de , gerado pela corrente que passa por corresponderá ao campo magnético no centro do anel e será, aproximadamente:
Que corresponde ao campo magnético no centro do anel.
O fluxo magnético no anel , então, será dado por:
Agora ficou fácil calcular a indutância mútua:
Como se trata apenas de um anel, . Simplificando a expressão acima:
Passo 2
No anel circula uma corrente . Calcule a força eletromotriz induzida no anel 1 pelo anel 2.
Se o cara falou de fem induzida, temos que pensar logo em Lei de Faraday, que é dada por:
Esse é um meio de resolver o problema. Um outra forma de resolver é utilizando a definição de indutância mútua na Lei de Faraday:
Como trata-se apenas de um anel e a Lei de Faraday pode ser reescrita como:
Esse meio de resolver, nesse caso, vai facilitar a nossa vida porque nós já calculamos a indutância mútua . Então vamos seguir com ela.
Resposta