Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 32
32- Um anel metálico de é colocado entre os pólos norte e sul de grandes ímãs, cujos planos da área são perpendiculares ao campo magnético. Esses ímãs produzem um campo inicial uniforme de entre eles, mas são gradualmente separados fazendo com que esse campo permaneça uniforme, mas diminua regularmente em .
Qual é o módulo do campo elétrico induzido no anel?
Em qual sentido (horário ou anti-horário) a corrente flui, do ponto de vista de alguém no pólo sul do ímã?
Passo 1
Pela lei de Faraday sabemos que:
Onde e como temos um anel de raio uniforme de área igual a então:
E considerando o campo elétrico uniforme nós temos que o comprimento do anel é igual a , então:
Logo:
Como o campo magnético diminui a uma taxa de então , nos dando um campo elétrico de (para um raio de anel de ):
Passo 2
A situação que temos na questão é essa aqui:
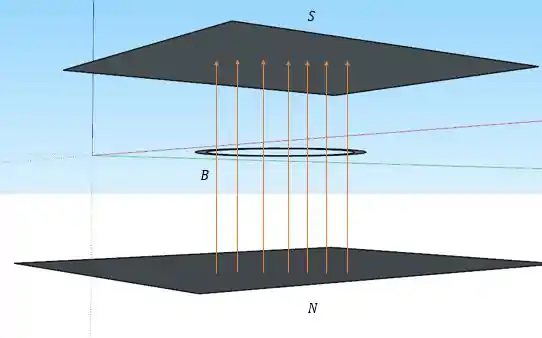
E a medida que o tempo passa as placas se separam diminuindo o campo magnético no anel, e como diminui pela Lei de Lenz o campo magnético induzido no anel é de querer fazer com que o campo magnético inicial tenda a voltar (então ele atuará no mesmo sentido do desenhado na figura), então pela regra da mão direita temos que a corrente de indução será no sentido anti-horário.