Energia no MHS
Teoria
Show de bolinhas pessoal, vimos que um MHS se trata de um movimento que oscila periodicamente, como por exemplo um pêndulo ou um sistema massa-mola. Mas agora quando falamos sobre a energia contida dentro desses sistemas, como será que ela se comporta?! Onde mora?! Como vive?! O que come?! Hoje, no RepórterAí.
Belezoca pessoal, pra gente descobrir essas informações, vamos analisar um sistema massa-mola oscilando em MHS, ele começa passando pela posição de equilíbrio com velocidade :
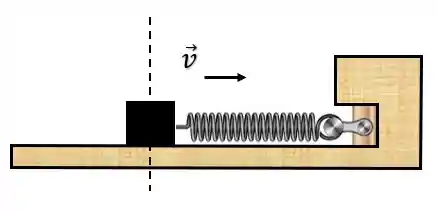
Até atingir a deformação máxima da mola, que chamamos de amplitude do MHS:
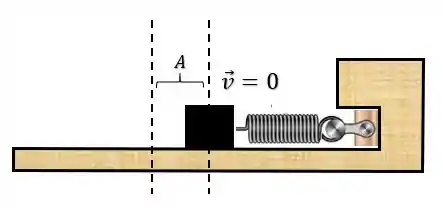
Nesse ponto o bloco para momentaneamente, de forma que a velocidade é nula. Depois disso, a velocidade inverte o sentido, e volta a passar pelo ponto de equilíbrio novamente, agora indo para o outro extremo:
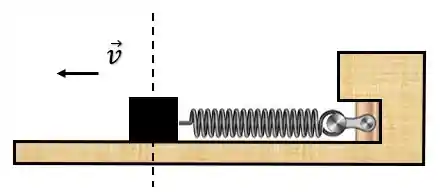
O bloco continua o movimento até atingir o outro extremo da mola, tal que:
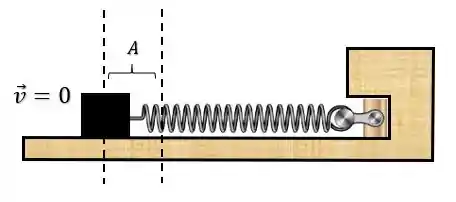
Oscilando periodicamente entre esses momentos. A malandragem aqui, é que a força que atua sobre esse sistema é a força elástica, que é uma força conservativa.
Mas calma aí chefia, porque isso quer dizer que a energia mecânica total contida no sistema se conserva. De forma que ela vai ser dada pela soma da energia cinética com a energia potencial :
Dessa forma, temos que a energia potencial elástica , será:
Onde é a constante elástica da mola enquanto é a deformação que a mola realiza. Além disso, temos que a energia cinética , pode ser escrita como:
Em que á massa do bloco e é a velocidade que ele se encontra. Logo:
Sendo assim, o bizu master aqui é a gente escolher um ponto para tentar descobrir a energia mecânica total do sistema. Por exemplo, se a gente pegar o momento do MHS onde a mola está completamente comprimida:
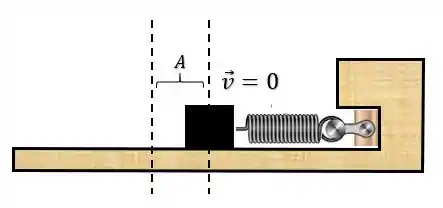
Nesse momento a energia cinética é mínima, devido a velocidade ser nula, entretanto a energia potencial elástica é máxima, afinal a mola está completamente comprimida. Então pela equação da energia mecânica, teremos:
Logo:
Isso quer dizer que podemos reescrever a equação da conservação da energia como:
Essa é a equação da conservação da energia pro MHS.
Agora, vamos observar como a energia varia com a posição da nossa massa em MHS. Se a gente fizer um gráfico da energia cinética, teremos que:
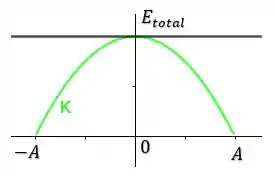
Ou seja, a energia cinética é máxima na posição de equilíbrio, e é mínima nos extremos. Agora se a gente montar um gráfico para a energia potencial, teremos que:
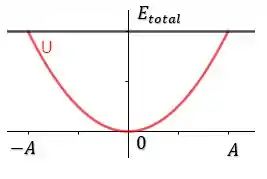
E podemos ver que ele é exatamente o oposto do gráfico da energia cinética, de forma que na posição de equilíbrio a energia potencial é mínimo enquanto que nos extremos ela será máxima.
Agora um exemplinho só pra gente fechar com chave de ouro.
Suponha que um bloco de massa oscila em MHS com uma mola de constante elástica . A amplitude do movimento é de , calcule sua velocidade quando o bloco passar por um ponto que equivale a metade da amplitude.
Então saca só galerinha, a equação da conservação da energia que encontramos, é dada como:
Substituindo os valores que o enunciado nos deu, teremos que:
O ponto que queremos medir a velocidade, é em:
Logo:
O sinal de indica duas repostas possíveis, uma negativa e uma positiva, o que faz sentido afinal o bloco passa pela metade da amplitude tanto na ida quanto na volta.
Então feshow de bola galerinha, bora lá fazer umas questõezinhas pra ver se a gente tá sabendo mesmo!!
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 108-27
Determine a energia mecânica de um sistema bloco-mola com uma constante de e uma amplitude de oscilação de
Passo 1
Bom, aqui a gente vai usar a equação:
Passo 2
Mas veja só: o enunciado te pediu a energia mecânica do sistema...ou seja, a energia total!
Isso equivale a dizer que ele está pedindo a soma:
Porém, podemos usar o lado esquerdo da equação e calcular a energia mecânica do sistema usando a amplitude máxima:
Passo 3
Show? Agora só aplicar os valores do enunciado.
No entanto, você deve ter percebido que os valores não estão em metros.
Vamos converter as unidades antes, então:
E:
Agora sim:
Resposta
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 108-28
Um sistema oscilatório bloco-mola possui uma energia mecânica de J uma amplitude de e uma velocidade máxima de . Determine:
(a) a constante elástica
(b) a massa do bloco
(c) a frequência da oscilação.
Passo 1
a)
Nessa primeira letra a gente pode usar a relação:
Lembra?
E representa a energia mecânica do sistema, ou seja, a sua energia total.
Bom, temos o valor da energia mecânica e temos o , fica fácil achar
Passo 2
b):
Aqui a gente vai ter que pensar um pouco diferente.
O enunciado nos deu a velocidade máxima do bloco. O que acontece com a energia mecânica quando o bloco atinge a velocidade máxima?
A energia mecânica se torna toda cinética. Ou seja:
Sacou? Não há energia potencial, nesse caso.
Novamente, temos todos os dados necessários pra achar
Passo 3
c)
Pra achar a frequência, basta a gente usar a relação:
Aplicando os valores:
Essa é a frequência angular. A linear será:
Resposta
a)
b)
c)
Exercício Resolvido #3
UFRJ-P2-2014.2-Q6
No momento em que começa a ser observada (, uma partícula de massa ligada a uma mola ideal de constante se afasta da origem e sua energia potencial vale metade da energia mecânica total. Sobre sua constante de fase , podemos afirmar que:
Passo 1
Podemos descrever o movimento de um MHS com a equação:
Queremos descobrir informações sobre a sua constante de fase a partir de informações de sua energia.
Passo 2
O enunciado nos diz que quando o tempo vale zero, a energia potencial vale a metade da energia mecânica total.
Bom, a energia potencial é dada por:
Onde
E a energia mecânica total dada por:
Pois é o maior deslocamento possível pra partícula do MHS.
Como a energia potencial é igual à metade a energia mecânica total, quando , temos que:
Passo 3
Sendo , vamos comparar o valor de achado com a expressão do deslocamento:
No entanto, só existe a opção
Resposta
b)
Exercício Resolvido #4
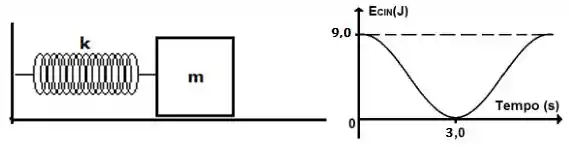
Um sistema massa-mola é colocado pra oscilar de modo que o gráfico abaixo mostra a energia cinética do bloco em função do tempo. Sabendo que a massa do sistema é M = 10Kg, qual é a amplitude do movimento em metros?
(a)
(b)
(c)
(d)
(e)
Passo 1
Bom, se já chegamos até aqui, já sabemos que um bloquinho como esse conectado a uma mola realiza um movimento harmônico simples (MHS).
Show de bola... E pelo princípio de conservação da energia mecânica, sabemos que a energia total mecânica (cinética + potencial) desse sistema é constante.
Mais um show de bola... E quando a mola está completamente esticada, sabemos que é máxima e é nula.
Olha o show de bola novamente... E quando a mola está completamente relaxada, é nula e é máxima.
Show de bolas
Looogo,
E a energia potencial:
Então:
Onde A é o deslocamento máximo, ou seja, amplitude que queremos determinar.
Passo 2
Do gráfico, :
Passo 3
Opa! Cancela o Show de bolas! Mas como podemos usar o k ali na fórmula???
Pode voltar com o Show de bolas... Nós vamos te dar o caminho...
Bom, do gráfico podemos determinaro período da onda, pois de um máximo até um mínimo de energia cinética temos um tempo de 3 segundos. Quando a mola está completamente esticada, temos um mínimo de energia cinética; quando ela passa pelo ponto de equilíbrio, temos um máximo de energia cinética. Isso corresponde a do movimento total... Então o período da onda será:
No MHS, temos que:
Substituindo na amplitude:
Como kg e :
Resposta
(b)
Exercício Resolvido #5
USP-P1-2009-Q3
Um oscilador harmônico possui frequência e amplitude
- Quais são os valores dos módulos da posição e da velocidade quando a energia potencial elástica for igual a energia cinética? (Suponha que no momento de equilíbrio)
- Quantas vezes isso ocorre em cada ciclo? Qual é o intervalo de tempo entre duas ocorrências?
- No momento em que o deslocamento é qual a fração da energia total do sistema referente a energia cinética e a qual corresponde a energia potencial?
Passo 1
Bom, galera, aqui vamos usar as equações de energia do MHS. Ou seja:
Além disso, vamos usar também a equação da posição em função do tempo:
E da velocidade ( derivada da função acima):
Simbora!
Passo 2
a)
Aqui a gente encontra uma situação onde a energia cinética é igual a energia potencial. Isso é:
Por outro lado, como a energia potencial é igual a cinética:
Lembrando que :
Passo 3
b)
Lembrando que, em um ciclo, a partícula se move de até e depois volta de para . Então, usando o resultado do item anterior:
A energia cinética se iguala a energia potencial quatro vezes vezes no ciclo.
Passo 4
Beleza, agora nós queremos saber a diferença de tempo entre as duas ocorrências . Como faremos isso? Usando a função que define a posição em função do tempo:
Vamos supor que em o corpo esteja em Então:
Beleza, então a função é:
Agora vamos descobrir o tempo e em que ocorre primeiro e . Assim:
Ali a gente só percebeu que o ângulo que gera um cosseno igual a é o .
Fazendo a mesma coisa com a outra posição:
Então, o tempo que estamos procurando será:
Passo 5
c)
Bom, pra calcular a energia potencial é simples:
E pra calcular a fração:
Beleza! Agora, pra calcular a fração de energia cinética, basta subtrair esse valor de 1:
Resposta
a)
b)
c)