Resolução e Dispersão de uma Rede de Difração
Produzido por Bruno SoaresTeoria
Resolução de uma Rede de Difração
A rede de difração consegue separar os diferentes comprimentos de onda que existem na luz branca em linhas de diferentes cores. Porém, como tudo na vida, existe um limite.
Cada rede de difração tem uma variação mínima de comprimento de onda que ela consegue separar.
Se uma dada rede conseguir separar luz com comprimentos de onda e , a resolução dela é dada por:
Onde
É o comprimento de onda médio.
Ou seja, ela consegue resolver uma variação de partes do comprimento de onda.
A menor variação de comprimentos de onda que uma rede consegue determinar é descrita pelo poder de resolução cromático , dado por:
Onde é a média dos dois comprimentos de onda que você deseja separar, é o número de fendas da rede de difração e é a ordem das linhas espectrais.
Fisicamente, a resolução é uma medida da largura das franjas de difração de diferentes comprimentos de onda.
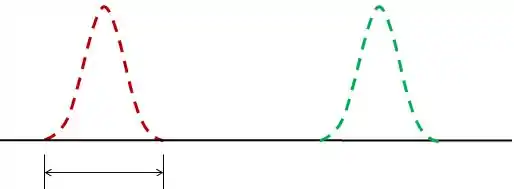
Além disso, o motivo de termos é o critério de Rayleigh:

A distância angular entre dois máximos de um comprimento de onda é da ordem de , pois:
Mas como essa distância corresponde a N-1 mínima, a gente pode dizer que a distância do primeiro mínimo depois de um máximo principal é algo na ordem de
Além disso, a distância entre a linha de ordem da luz de comprimento de onda e é da ordem de , pois:
Assim, igualando os dois pelo critério de Rayleigh, temos:
Dispersão de uma Rede de Difração
A resolução da rede de difração é uma medida da largura das franjas de interferência, e de o quanto conseguimos distinguir duas cores diferentes.
Mas além dessa largura, tem mais uma coisa que nos permite distinguir as linhas das duas cores: a distância entre essas linhas.
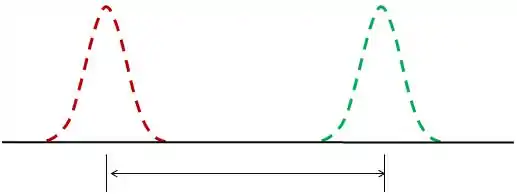
O que usamos como medida de o quanto uma rede afasta franjas de diferentes cores é a dispersão.
O afastamento das franjas é a variação do desvio angular delas.
A diferença de cores é a variação do comprimento de onda.
Vamos definir a dispersão como a razão entre as duas variações: A dispersão de uma rede é a variação do desvio angular para uma dada variação de comprimento de onda.
Para uma variação muito pequena de , se torna a derivada do desvio angular pelo comprimento de onda da luz.
Da definição tira-se uma fórmula mais prática para o cálculo de :
Vejamos então a dispersão para uma rede de difração com , distância de de distância entre duas fendas consecutivas.
Qual vai ser a dispersão para as linhas de ordem 2 se eu usar luz vermelha ()?
Primeiro, o ângulo para essa linha vai ser dada por:
Com isso:
Como ângulo não tem unidade, a unidade da dispersão vai ser
Dispersão de uma Rede de Difração
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 143-83
Um feixe luminoso que contém uma faixa estreita de frequências em torno de incide perpendicularmente em uma rede de difração com uma largura de e uma densidade de linhas de .
Para essa luz, qual é a menor diferença de comprimentos de onda que a rede é capaz de resolver em terceira ordem?
Passo 1
A menor diferença percentual que a rede é capaz de resolver é medida pela resolução da rede. A resolução de uma rede é, de fato, o inverso dessa diferença percentual.
Assim, para acharmos a diferença de comprimentos de onda que a rede é capaz de resolver, temos:
Passo 2
A resolução de uma rede de difração em uma ordem é dada por:
Onde é o número de fendas da rede. Para acharmos esse valor, nós fazemos a largura da rede multiplicada pela densidade de linhas dela.
Como queremos ver a resolução para terceira ordem:
Passo 3
Por fim, a luz que estamos avaliando tem comprimento de onda .
Resposta
A menor diferença de comprimentos de onda que a rede é capaz de resolver em terceira ordem é
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-88
Um feixe luminoso contém dois comprimentos de onda, e , que devem ser resolvidos com uma rede de difração.
Se a largura da rede é , qual é o número mínimo de linhas necessário para que os dois comprimentos de onda sejam resolvidos em segunda ordem?
Passo 1
Para esses dois comprimentos de onda, a média é:
E a diferença dos comprimentos de onda é:
Assim, a resolução é:
Passo 2
Outra fórmula para resolução é:
Logo, o número de linhas necessária para essa resolução em segunda ordem () é:
Cuidado!
Nessa questão tinha uma pegadinha: Em nenhum momento nós usamos a largura da rede. Ela foi uma informação dada que não era necessária.
Resposta
Exercício Resolvido #3
PUC-Rio, Física 4, Prova 2, 2013.2, 3II
A luz de uma lâmpada de sódio, com um comprimento de onda , incide perpendicularmente em uma rede de difração com em de largura.
Determine a Dispersão da rede em segunda ordem.
Passo 1
Temos que a dispersão é dada pela seguinte fórmula:
Para determinar , precisamos primeiro determinar para segunda ordem, para isso, utilizaremos a seguinte fórmula:
Lembrando que , temos:
Passo 2
Voltando à fórmula da dispersão, temos:
Substituindo, temos:
Resposta
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-101
Mostre que a dispersão de uma rede de difração é dada por:
Passo 1
Para uma rede de difração, temos que:
Usando como a ordem da primeira franja de interferência, essa ordem vai ser:
Substituindo:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-95
Uma rede de difração tem uma resolução .
- Mostre que a diferença de frequências que se encontra no limite da resolução, , é dada por .
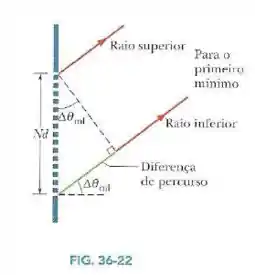
- Para a Fig. 36-22, mostre que a diferença entre os tempos de percurso do raio de baixo e do raio de cima é dada por .
- Mostre que e, portanto, esse produto não depende dos parâmetros da rede. Suponha que .
Passo 1
Letra a)
Para transformar de comprimento de onda em frequência, nós usamos a velocidade da luz:
Assim:
Passo 2
Substituindo o valor nas fórmulas de resolução:
Considerando que , podemos escrever:
Considerando que é muito pequeno, podemos desprezá-lo nas equações e fazer:
De uma forma mais exata, poderíamos usar direto a fórmula do e fazer:
Que recai na anterior se aproximarmos:
Passo 3
Letra b)
Pela figura dada, podemos ver que a diferença de percurso entre os raios do topo e de baixo é:
Quando temos fendas, a distância entre a superior e a de baixo é mas, quando é muito grande, podemos aproximar por .
Seja o percurso de cima e o percurso de baixo. Com a velocidade da luz sendo , os tempos são dados por:
Passo 4
Letra c)
Multiplicando os dois:
Como estamos olhando a resolução das franjas de interferência, nesse caso temos, para ambos e que vale a condição de máximo:
Usando a nossa aproximação de desprezível, podemos dizer que:
Que também nos faz dizer que .
Temos finalmente:
Resposta
Ei, a resposta está no passo a passo :)