Difração por N Fendas
Produzido por Bruno SoaresTeoria
Onde pode 2, pode 3 e pode o bonde!
A difração por um número qualquer de fendas não pontuais é muito parecida com a de duas fendas. Dessa vez vai ser como se fosse o produto da interferência por fendas com a difração por uma fenda não pontual.
Figura de difração para uma fenda simples de largura :
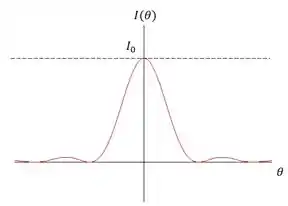
Figura de interferência para fendas separadas por uma distância :
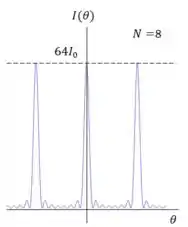
Para a difração por N fendas, a razão entre a intensidade de um ponto e a intensidade máxima da figura agora vai ser:
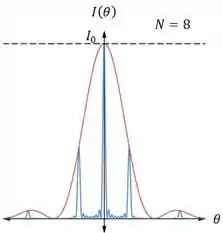
Os máximos principais da figura continuam no mesmo lugar que os máximos da figura de interferência de duas fendas. Eles são calculados pela relação:
Quando iluminamos a rede com uma luz monocromática de raios paralelos, a figura obtida é constituída por uma série de linhas em ângulos determinados pela equação acima.
Lembrando algumas informações muito importantes:
- Existem máximos secundários entre cada par de máximos principais.
- Existem mínimos entre cada par de máximos principais, esses pontos são encontrados quando , .
- A intensidade máxima da figura acontece na franja central, e é dada por , onde é a intensidade da luz incidente e é o número de fendas.