Radiação do Corpo Negro

Teoria

Quando enxergamos um objeto, o que enxergamos é a luz que vem dele pra gente.

Parte disso vem da luz que incide no objeto. Essa luz incidente tem uma parte que é absorvida pelo objeto e parte refletida. A cor que enxergamos no objeto são os comprimentos de onda refletidos por ele.

No caso de objetos pretos, teoricamente todas as cores seriam absorvidas e nenhuma refletida (na prática sempre tem alguma luz refletida).

A outra parte da luz que enxergamos é irradiada do próprio objeto.

Quando você esquenta um metal ou rochas a temperaturas extremamente altas, pode-se notar uma mudança na cor do metal. Ele começa a ficar vermelho e depois vai ficando meio azulado a medida que sua temperatura aumenta.

Essa mudança é o metal emitindo vários comprimentos de onda para uma dada temperatura, mas com um pico de emissão em um desses comprimentos.

Olha a cor avermelhada da Lava por exemplo.

Uma superfície que seja uma absorvedora perfeita (ou seja, que não reflete nada) também é o melhor emissor de luz para qualquer cor possível e ela é chamada de corpo negro.

Espectro de emissão do Corpo Negro

Embora corpos negros não existam na vida real, existem formas de chegar muito perto de o que seria um corpo negro com alguns experimentos de laboratório.

Por isso é possível determinar experimentalmente qual seria a intensidade da luz emitida por um corpo negro em função do comprimento de onda (da “cor”) da luz. Seria mais ou menos assim:

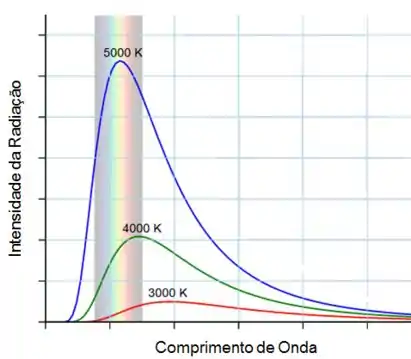
(Esse gráfico não está em escala)

Durante algum tempo os físicos não conseguiram explicar a teoria por trás dessas curvas.

Foi Planck com sua hipótese de quantização da energia que finalmente conseguiu explicá-las, chegando a uma fórmula para essas curvas.

Nessa fórmula, é a constante de Planck, é a velocidade da luz no vácuo, é uma constante chamada constante de Boltzmann (, é o comprimento de onda da luz emitida, é a temperatura do corpo negro e é a intensidade da radiação.

Às vezes essa fórmula é chamada de Lei da Radiação de Planck.

Lei de Stefan-Boltzmann

Da lei da radiação de Planck é possível deduzir corretamente outros dois resultados que não tinham explicação. O primeiro deles é chamado Lei de Stefan-Boltzmann, e diz que:

Que significa que a intensidade luminosa total emitida pelo corpo negro é proporcional à quarta potência da sua temperatura. A constante de proporcionalidade é chamada constante de Stefan-Boltzmann.

Essa lei é obtida integrando a lei de Planck em todos os comprimentos de onda (de a ). Sim, essa integral é tão trabalhosa quanto parece. Não, eu sequer tentei integrar e só confiei nos livros de física. Um dia eu integro isso... talvez...

Com essa integração, pode-se observar que:

Lei de Wien

O segundo resultado é a Lei de Wien.

A lei de Wien relaciona o comprimento de onda máximo de emissão do corpo negro em função da temperatura. Ela diz que o produto desse comprimento de onda pela temperatura é dado por uma constante:

Repare que a constante está dada em metros Kelvin. Desse modo, temos sempre que utilizar essas unidades!

Não se preocupe, o valor dessa constante é geralmente dado nas provas.

Ela também pode ser deduzida da lei de Planck. Você deriva a fórmula e iguala a zero. O comprimento de onda correspondente vai ser:

Agora vamos praticar?

Espectro de emissão do Corpo Negro

Lei de Stefan-Boltzmann

Lei de Wien

Exercícios Resolvidos

Exercício Resolvido #1

PUC-RIO, Física 4, Prova 3, 2012.2.

Considere o uso da lei de Wien () válido aproximadamente para a pele humana. Admita a temperatura da pele .

Determine o comprimento de onda dessa radiação. Diga se está na faixa do visível (

Passo 1

Sabendo que o valor dessa constante é dado por:

Calma....essa constante é normalmente dada na capa da prova!

Como estamos trabalhando no S.I, devemos passar a temperatura da superfície de Celsius para Kelvins:

Passo 2

Agora podemos calcular o comprimento de onda máximo! Se liga:

substituindo o valor da temperatura, temos:

Portanto, não está na faixa do visível.

Resposta

Não está na faixa do visível pois .

Exercício Resolvido #2

PUC-RIO, Física 4, Prova 3, 2013.2

Observe as curvas de Planck da radiação de corpo negro na figura abaixo. Compare-as. Se a temperatura de emissão da radiação aumenta, diga o que ocorre com o comprimento de onda emitido quando a intensidade é máxima.

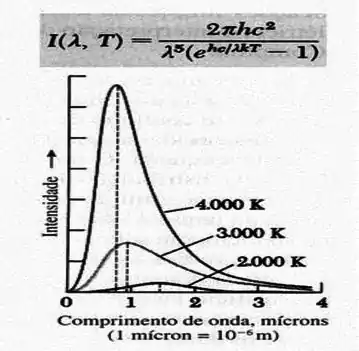
Passo 1

Vamos agora analisar separadamente as curvas apresentadas no gráfico.

Para uma temperatura de emissão de , temos que a radiação possui intensidade máxima para um comprimento de onde de . Ao subirmos a temperatura de emissão para , percebemos que a radiação possui intensidade máxima para um comprimento de onda de . Ao aumentarmos mais uma vez a temperatura de emissão, dessa vez para , vemos que a radiação possuirá intensidade máxima para um comprimento de onda menor.