Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Efeito Compton

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos trocar uma ideia sobre o Efeito Compton. A ideia é descobrir como esse cara nos ajuda a entender a perda de energia da luz quando ela se espalha!

⭐ Veja também ⭐

O que é o Espalhamento Compton?

Não sei se você já chegou a se deparar com o conceito da dualidade onda-partícula da luz. Ele diz que a luz pode se comportar ora como onda eletromagnética, ora como partícula. Se a luz se comporta como partícula, ela pode se chocar com outras partículas!

O Efeito, ou Espalhamento Compton, explica a interação entre fótons e elétrons livres como um processo no qual a luz se espalha e cede energia pro elétron na forma de energia cinética.

As colisões entre essas partículas são tratadas como elásticas. Então, podemos analisá-las pela conservação do momento linear e da energia.

A equação que usamos para o espalhamento Compton é a seguinte:

👉 é a variação entre o comprimento de onda do fóton antes e depois do espalhamento.

👉 é a massa do elétron.

👉 é a constante de Planck.

👉 é a velocidade da luz no vácuo.

👉 é o ângulo de reflexão do fóton.

Energia do Fóton após o Espalhamento

Se liga no diagrama desse fenômeno de espalhamento:

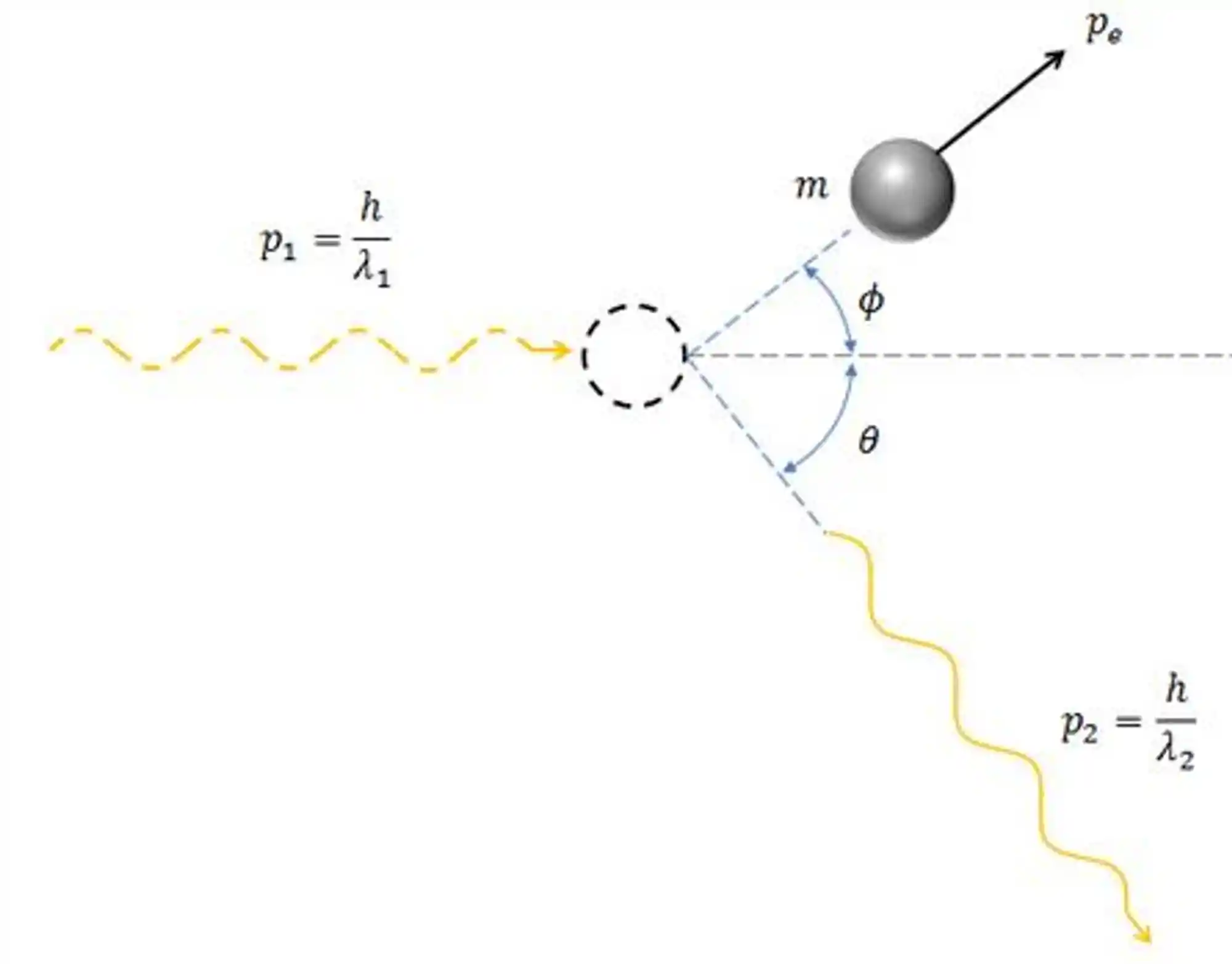
Espalhamento Compton.
Espalhamento Compton.

Se reparar na imagem e no que discutimos anteriormente, vai ver que o comprimento de onda do fóton muda de um momento para o outro. Isso significa que a energia do fóton também varia.

A energia perdida pelo fóton vai ser absorvida pela partícula na forma de energia cinética. Logo, podemos escrever a variação de energia cinética para essa outra partícula:

ó

Atenção: essa não vai ser a energia total da partícula, é simplesmente a energia absorvida devido à colisão com o fóton.

Tranquilo? Bora seguir com alguns exercícios para entendermos como isso aí pode ser cobrado na sua provinha.

Energia do Fóton após o Espalhamento

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-33, modificado.

Determine o comprimento de onda de Compton:

  1. De um elétron.
  2. De um próton.

Qual é a energia dos fótons de uma onda eletromagnética com um comprimento de onda igual ao comprimento de onda de Compton

  1. Do elétron.
  2. Do próton.

Dê a energia em J e em M e V

Dados:

Massa do elétron m e = 9,109 ∙ 10 - 31 K g

Massa do próton m p = 1,673 ∙ 10 - 27 K g

Passo 1

O comprimento de onda de Compton de uma partícula é:

h m c

Onde:

  • h = 6,626 ∙ 10 - 34   J ∙ s é a constante de Planck.
  • c = 2,998 ∙ 10 8   m / s é a velocidade da luz no vácuo.
  • m é a massa da partícula.

Passo 2

Letra a)

A massa do elétron é:

m e = 9,109 ∙ 10 - 31 K g

Logo:

h m e c = 6,626 ∙ 10 - 34 9,109 ∙ 10 - 31 ∙ 2,998 ∙ 10 8 ≅ 2,426 ∙ 10 - 12   m

Passo 3

Letra b)

A massa do próton é:

m p = 1,673 ∙ 10 - 27 K g

Logo:

h m p c = 6,626 ∙ 10 - 34 1,673 ∙ 10 - 27 ∙ 2,998 ∙ 10 8 ≅ 1,321 ∙ 10 - 15   m

Passo 4

Letra c)

A energia do fóton é dada por:

E = h f = h c λ

Para um fóton com comprimento de onda de Compton do elétron:

E = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 2,426 ∙ 10 - 12 ≅ 8,188 ∙ 10 - 14   J

A conversão de J para e V é:

1   e V = 1,602 ∙ 10 - 19   J

E = 8,188 ∙ 10 - 14 1,602 ∙ 10 - 19 ≅ 5,11 ∙ 10 5   e V = 0,511   M e V

Passo 5

Letra d)

A energia do fóton é dada por:

E = h f = h c λ

Para um fóton com comprimento de onda de Compton do próton:

E = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 1,321 ∙ 10 - 15 ≅ 1,504 ∙ 10 - 10   J

A conversão de J para e V é:

1   e V = 1,602 ∙ 10 - 19   J

E = 1,504 ∙ 10 - 10 1,602 ∙ 10 - 19 ≅ 9,388 ∙ 10 8   e V = 938,8   M e V

Resposta

Letra a)

h m e c ≅ 2,426 ∙ 10 - 12   m

Letra b)

h m p c ≅ 1,321 ∙ 10 - 15   m

Letra c)

E ≅ 8,188 ∙ 10 - 14   J ≅ 0,511   M e V

Letra d)

E ≅ 1,504 ∙ 10 - 10   J ≅ 938,8   M e V

Exercício Resolvido #2

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 207-8.

Espalhamento de Compton.

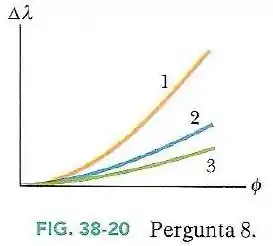
A Fig.38-20 mostra o deslocamento de Compton Δ λ em função do ângulo de espalhamento ϕ para três diferentes partículas estacionárias usadas como alvo.

Coloque as partículas na ordem de suas massas, começando pela maior.

Passo 1

O deslocamento de Compton em função do ângulo de espalhamento é dado por:

Δ λ = h m c ( 1 - cos ⁡ ϕ )

De ϕ = 0 até ϕ = π , o cosseno varia de 1 até - 1 , fazendo o deslocamento aumentar a medida que o ângulo de espalhamento aumenta.

A medida de o quanto o ângulo de espalhamento afeta o deslocamento de Compton é dado pelo comprimento de onda de Compton da partícula:

λ C = h m c

Quanto maior o comprimento de onda de Compton mais o deslocamento aumenta com o ângulo.

Assim, pelo gráfico, temos:

λ C , 1 > λ C , 2 > λ C , 3

Passo 2

O comprimento de onda de Compton é inversamente proporcional à massa da partícula.

λ C = h m c

Quanto maior esse valor, menor é a massa da partícula. Logo:

m 1 < m 2 < m 3

Começando pela maior, a ordem das massas das partículas é:

m 3 > m 2 > m 1

Resposta

m 3 > m 2 > m 1

Exercício Resolvido #3

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 209-29.

Um feixe luminoso com um comprimento de onda de 2,4   p m incide em um alvo que contém elétrons livres.

  1. Determine o comprimento de onda da luz espalhada a 30 ° com a direção do feixe incidente.
  2. Faça o mesmo para um ângulo de espalhamento de 120 ° .

Passo 1

O deslocamento Compton da luz espalhada é:

Δ λ = λ C ,   e ( 1 - cos ⁡ ϕ )

Onde λ C , e = h / m e c é o comprimento de onda de Compton do Elétron, cuja massa é m e = 9,109 ∙ 10 - 31 K g . O comprimento de onda de Compton do Elétron fica:

λ C , e = h m e c = 6,626 ∙ 10 - 34 9,109 ∙ 10 - 31 ∙ 2,998 ∙ 10 8 ≅ 2,426 ∙ 10 - 12   m

Como 1   p m = 10 - 12 m , teremos:

λ C , e ≅ 2,426   p m

Passo 2

Letra a)

Para ϕ = 30 ° = π 6   r a d , temos:

cos ⁡ ϕ = 3 2

Δ λ ≅ 2,426 ∙ 1 - 3 2 ≅ 2,426 ∙ 2 - 3 2 ≅ 2,426 ∙ 0,134 ≅ 0,325   p m

O comprimento de onda da luz espalhada vai ser o da incidente somado do deslocamento:

λ ' = λ + Δ λ

Pelo enunciado, λ = 2,4   p m .

λ ' = 2,4 + 0,325 = 2,725   p m

Passo 3

Letra b)

Para ϕ = 120 ° = 2 π 3   r a d , temos:

cos ⁡ ϕ = - 1 2

Δ λ ≅ 2,426 ∙ 1 - - 1 2 = 2,426 ∙ 1 + 1 2 2,426 ∙ 3 2 ≅ 3,639   p m

O comprimento de onda da luz espalhada vai ser o da incidente somado do deslocamento:

λ ' = λ + Δ λ

Pelo enunciado, λ ' = 2,4   p m .

λ ' = 2,4 + 3,639 = 6,039   p m

Resposta

Letra a)

λ ' = 2,725   p m

Letra b)

λ ' = 6,039   p m

Exercício Resolvido #4

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-37.

Que aumento percentual do comprimento de onda leva a uma perda de 75 % da energia do fóton em uma colisão entre um fóton e um elétron livre?

Passo 1

A energia de um fóton é dada por:

E = h c λ

Depois da colisão, ele sofre uma perda de 75 % da energia do fóton, e fica com uma energia:

E ' = 0,25 ∙ E

O que corresponde a:

h c λ ' = 0,25 ∙ h c λ → λ 0,25 = λ '

Ou seja:

λ ' = 4 ∙ λ

Passo 2

O aumento percentual do comprimento de onda é:

Δ λ = λ ' - λ λ = 3 λ λ = 3

O que corresponde a um aumento de 300 % no comprimento de onda.

Resposta

Um aumento de 300 % no comprimento de onda.

Exercício Resolvido #5

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 213-38.39.

Se um fóton com 0,0425   n m de comprimento de onda se choca com um elétron livre e sobre um espalhamento que forma um ângulo de 35,0 ° com sua direção original, calcule:

  1. A variação no comprimento de onda desse fóton;
  2. O comprimento de onda da luz espalhada;
  3. A variação de energia do fóton (há perda ou ganho?);
  4. A energia ganha pelo elétron;

Passo 1

Trata-se de um problema de espalhamento Compton, onde a equação é dada por:

λ 2 - λ 1 = h m c   1 - cos ⁡ θ

Passo 2

Letra (a): Calcule a variação no comprimento de onda desse fóton.

Δ λ = λ 2 - λ 1 = h m c   1 - cos ⁡ θ

Onde:

h / m c = 2,426 × 10 - 12 m ;

θ = 35 ° ;

cos ⁡ 35 ° = 0,82 ;

Logo:

Δ λ = 2,426 × 10 - 12 × 1 - 0,82

Δ λ = 0,439 × 10 - 12 = 4,39 × 10 - 4   n m

Passo 3

Letra (b): Calcule o comprimento de onda da luz espalhada.

Δ λ = λ 2 - λ 1

λ 2 = λ 1 + Δ λ

Onde:

λ 1 = 0,0425   n m = 4,25 × 10 - 11   m ;

Δ λ = 4,39 × 10 - 4   n m ≅ 0,00044   n m ;

Logo:

λ 2 = 0,0425 + 0,00044

λ 2 = 0,04294   n m

Passo 4

Letra (c): Calcule a variação de energia do fóton (há perda ou ganho?);

A energia do fóton é dada por:

E = h f = h c λ

Passo 5

A variação da energia do fóton será dada por:

Δ E f = E 2 - E 1 = h c 1 λ 2 - 1 λ 1

Onde:

h = 4,136 × 10 - 15   e V   s ;

c = 3 × 10 8   m / s ;

λ 2 = 0,04294   n m = 4,294 × 10 - 11   m ;

λ 1 = 0,0425   n m = 4,25 × 10 - 11   m ;

Logo:

Δ E f = 4,136 × 10 - 15 × 3 × 10 8 × 1 4,294 × 10 - 11 - 1 4,25 × 10 - 11

Δ E = - 300   e V

Há perda de energia.

Passo 6

Letra (d): Calcule a energia ganha pelo elétron.

A energia ganha pelo elétron é igual à energia perdida pelo fóton. Assim:

Δ E e = - Δ E f = + 300   e V

Resposta

Letra (a):

4,39 × 10 - 4   n m

Letra (b):

0,04294   n m

Letra (c):

Δ E r = - 300   e V

Letra (d):

Δ E e = + 300   e V

Exercício Resolvido #6

PUC-RIO, Física 4, Prova 3, 2012.2.

I

Um feixe de raios gama com fótons de energia 0,511   M e V incide sobre um alvo de alumínio, sendo espalhado em várias direções por elétrons quase livres do alvo.

a ) Calcule o comprimento de onda dos raios gama incidentes.

b ) Determine o comprimento de onda dos raios gama espalhados a 90 ° em relação à direção do feixe incidente.

c ) Obtenha a energia dos elétrons espalhados quando os fótons são espalhados a 90 ° .

Passo 1

a )

Para determinar o comprimento de onda, devemos lembrar da definição para a energia dos fótons:

E = h . f

Substituindo f por c / λ   , temos:

E = h . c λ

Substituindo o valor da energia, assim como o valor da constante h . c = 1240   e V .   n m , temos:

0,511 × 10 6 = 1240 λ

Perceba que tivemos que passar a energia de M e V para e V .

λ 0 = 0,002427   n m

Passo 2

b )

Para o Efeito Compton, temos que a variação do comprimento de onda é dada por:

Δ λ = h m . c   1 - cos ⁡ θ

λ - λ 0 = h m . c 1 - cos ⁡ θ

Substituindo os valores dados, assim como os valores das constantes, temos:

λ - 0,002427 = 0,00243 ( 1 - cos ⁡ 90 ° )

O valor h m e . c = 0,00243   n m , é geralmente fornecido.

λ = 0,004857   n m

Passo 3

c )

Agora, vamos determinar a energia total dos elétrons espalhados. Para isso, vamos utilizar a conservação da energia durante a colisão. Sabendo que antes, temos somente a energia dos fótons incidentes e a energia de repouso do elétron, e depois temos a energia dos fótons espalhados e a energia total dos elétrons, temos:

E f ó t o n s i + m e . c 2 = E f ó t o n s f + E e l é t r o n s

E f ó t o n s i + m e . c 2 = h . f + E e l é t r o n s

Substituindo f por c / λ , temos:

E f ó t o n s i + m e . c 2 = h . c λ + E e l é t r o n s

Substituindo os valores já obtidos, assim como os valores das constantes, temos:

0,511 × 10 6 + 0,511 × 10 6 = 1240 0,004857 + E e l é t r o n s

E e l é t r o n s = 0,511 × 10 6 + 0,511 × 10 6 - 0,255 × 10 6

E e l é t r o n s = 0,767   M e V    

Resposta

a ) λ 0 = 0,002427   n m

b ) λ = 0,004857   n m

c ) E e l é t r o n s = 0,767   M e V

Exercício Resolvido #7

UFRJ, Física 4, Prova 2, 2011.2.

Um estudante de Física IV decide calibrar um goniômetro (instrumento para medir ângulos) com o auxílio de uma fonte de raio X com λ 0 = 2,988   Å , um bloco de algum material e um analisador de comprimentos de onda.

Sabendo que a onda Compton é λ c = 0,024   Å , qual o ângulo deverá ser medido no goniômetro uma vez que o analisador mediu um comprimento de onda espalhado λ = 3   Å   .

  1. 30 °
  2. 45 °
  3. 60 °
  4. 75 °
  5. 90 °
  6. Nenhuma das anteriores.

Passo 1

Trata-se de um problema de espalhamento. Segundo Compton, podemos associar os comprimentos da onda incidente λ 1 e espalhado λ 2 por:

λ 2 - λ 1 = h m c   1 - cos ⁡ θ

Ou:

λ 2 - λ 1 = λ c   1 - cos ⁡ θ

Passo 2

λ 2 - λ 1 = λ c   1 - cos ⁡ θ

Onde:

λ 2 = λ = 3   Å ;

λ 1 = λ 0 = 2,988   Å ;

λ c = 0,024   Å ;

Logo:

cos ⁡ θ = 1 - λ 2 - λ 1 λ c

cos ⁡ θ = 1 - 3 - 2,988 0,024 = 0,5

θ = 60 °

Resposta

c) 60 °

Exercício Resolvido #8

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-32.

Um feixe de raios gama cujos fótons têm uma energia de 0,511   M e V incide em um alvo de alumínio e é espalhado em várias direções por elétrons quase livres do alvo.

  1. Qual é o comprimento de onda dos raios gama incidentes?
  2. Qual é o comprimento de onda dos raios gama espalhados a 90,0 ° com o feixe incidente?
  3. Qual é a energia dos fótons espalhados nessa direção?

Passo 1

Letra a)

A energia de um fóton de luz é dado por:

E = h c λ

Onde:

  • h = 4,136 ∙ 10 - 15   e V ∙ s
  • c = 2,998 ∙ 10 8   m / s

O enunciado nos diz que E = 0,511   M e V = 0,511 ∙ 10 6   e V . Rearrumando nossa equação:

λ = h c E = 4,136 ∙ 10 - 15 ∙ 2,998 ∙ 10 8 0,511 ∙ 10 6 = 24,266 ∙ 10 - 13   m ≅ 2,4266   p m

Passo 2

Letra b)

O deslocamento de Compton é dado por

Δ λ = λ C ,   e ( 1 - cos ⁡ ϕ )

Onde λ C , e = h / m e c é o comprimento de onda de Compton do Elétron, e a massa é m e = 9,109 ∙ 10 - 31 K g . O comprimento de onda de Compton do Elétron fica:

λ C , e = h m e c = 6,626 ∙ 10 - 34 9,109 ∙ 10 - 31 ∙ 2,998 ∙ 10 8 ≅ 2,426 ∙ 10 - 12   m

Como 1   p m = 10 - 12 m , teremos:

λ C , e ≅ 2,426   p m

Passo 3

Quando ϕ = 90 ° temos cos ⁡ ϕ = 0 e ficamos com:

Δ λ = 2,426 ∙ 1 - 0 = 2,426   p m

O comprimento de onda da luz espalhada vai ser o da incidente somado do deslocamento:

λ ' = λ + Δ λ

λ ' = 2,4266   + 2,426 ≅ 4,853   p m

Passo 4

Letra c)

A energia dos fótons espalhados nessa direção será:

E = h c λ ' = 4,136 ∙ 10 - 15 ∙ 2,998 ∙ 10 8 4,853 ∙ 10 - 12 ≅ 2,555 ∙ 10 5   e V = 0,2555   M e V

Em Joules essa energia ficaria:

E = 0,2555 ∙ 10 6 ∙ 1,602 ∙ 10 - 19 = 0,409 ∙ 10 - 13   J

Resposta

Letra a)

λ ≅ 2,4266   p m

Letra b)

λ ' ≅ 4,853   p m

Letra c)

E = 0,2555   M e V = 0,409 ∙ 10 - 13   J

Exercício Resolvido #9

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 210-30.

Um feixe de raios X com um comprimento de onda de 0,0100   n m , no sentido positivo do e i x o   x , incide em um alvo que contém elétrons quase livres.

Para o espalhamento de Compton a 180 ° de um fóton por um desses elétrons, determine:

  1. O deslocamento de Compton.
  2. A variação da energia do fóton.
  3. A energia cinética do elétron após o espalhamento.
  4. O ângulo entre o semi-eixo x positivo e a direção de movimento do elétron após o espalhamento.

Passo 1

Letra a)

O deslocamento de Compton é dado por:

Δ λ = h m c 1 - cos ⁡ ϕ

Para ϕ = 180 ° , temos cos ⁡ ϕ = - 1

Δ λ = h m c 1 - - 1 = 2 h m c

No caso do elétron:

h m e c ≅ 2,426 ∙ 10 - 12   m = 2,426   p m

E assim:

Δ λ = 2 ∙ 2,426 = 4,852   p m = 0,004852   n m

Passo 2

Letra b)

A energia inicial do fóton era de:

E = h c λ

Onde:

  • h ≅ 6,626 ∙ 10 - 34   J ∙ s
  • c ≅ 2,998 ∙ 10 8   m / s
  • λ = 0,0100   n m = 10 - 11   m (pelo enunciado)

E = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 10 - 11 ≅ 19,865 ∙ 10 - 15   J

O comprimento de onda do fóton após a interação vai ser:

λ ' = λ + Δ λ = 0,0100 + 0,004852 = 0,014852   n m = 1,4852 ∙ 10 - 11   m

E assim sua energia será:

E = 6,626 ∙ 10 - 34 ∙ 2,998 ∙ 10 8 1,4852 ∙ 10 - 11 ≅ 13,375 ∙ 10 - 15   J

A variação de energia fica:

Δ E = 13,375 ∙ 10 - 15 - 19,865 ∙ 10 - 15 = - 6,49 ∙ 10 - 15   J

Onde o sinal negativo indica que a energia foi perdida.

Passando para e V , ficamos com:

Δ E = - 6,49 ∙ 10 - 15 1,602 ∙ 10 - 19 = - 4,05 ∙ 10 4   e V = - 40,5   K e V

Passo 3

Letra c)

Toda a energia perdida pelo fóton é absorvida pelo elétron na forma de energia cinética. Por isso a energia cinética do elétron será igual ao módulo da variação de energia do fóton.

K e = 6,49 ∙ 10 - 15 J = 40,5   K e V

Passo 4

Letra d)

Quando o fóton se aproxima do elétron, o elétron está parado e, por isso, não tem momento linear. Já o fóton tem um momento linear com componente apenas na direção do semi-eixo x positivo.

Como o espalhamento do fóton é de 180 ° , o seu momento linear final tem componente apenas na direção do semi-eixo x negativo.

Por isso, o elétron adquire um momento linear apenas com componente no semi-eixo x positivo.

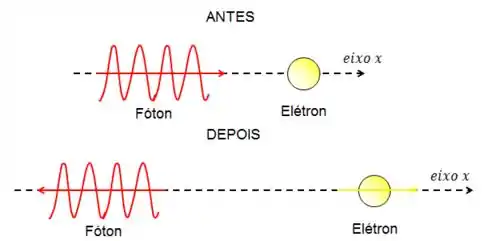
Isso significa que o ângulo θ entre o movimento do elétron e o semi-eixo x positivo é igual a zero.

θ = 0

Resposta

Letra a)

Δ λ = 4,852   p m = 0,004852   n m

Letra b)

Δ E = - 6,49 ∙ 10 - 15   J = - 40,5   K e V

Letra c)

K e = 6,49 ∙ 10 - 15 J = 40,5   K e V

Letra d)

θ = 0

Exercícios de Livros Relacionados

Um fóton incidente de energia Ei sofre espalhamento de Compton no ângulo de θ. Mostre que a energia Es do fóton espalhado é dada por E s = E i 1 + E i m e c 2 1 - cos ⁡ θ
Quando os fótons são dispersos por elétrons em uma amostra de carbono, a mudança no comprimento de onda é de 0,33 pm. Encontre o ângulo de dispersão. (Suponha que os elétrons estejam se movendo inicia
Durante um laboratório de física avançada, os alunos usam raios X para medir o comprimento de onda de Compton, λC. Os alunos obtêm os seguintes desvios de comprimento de onda λ2 - λ1 em função do ângu
Encontre a mudança no comprimento de onda dos fótons dispersos por elétrons estacionários livres em θ = 60 °. (Suponha que os elétrons estejam se movendo inicialmente a uma velocidade desprezível e es
Os fótons em um feixe monocromático são espalhados por elétrons. O comprimento de onda dos fótons dispersos em um ângulo de 135 ° com a direção do feixe de fótons incidentes é 2,3% menor que o comprim