Exercícios de Contração do Comprimento - Lista de Exercícios Resolvida

Em relação a um observador na Terra, a pista de lançamento de uma espaçonave possui comprimento de .

1. Qual é o comprimento da pista medido pelo piloto de uma espaçonave que se desloca com velocidade igual a em relação à Terra?
2. Uma observadora em repouso na Terra mede o intervalo de tempo desde o momento em que a espaçonave está diretamente sobre o início da pista até o instante em que a espaçonave está diretamente sobre o final da pista. Que resultado ela obtém?
3. O piloto da espaçonave mede o intervalo de tempo desde o momento em que espaçonave passa diretamente sobre o início da pista até o instante em que ela passa diretamente sobre o final da pista. Que resultado ele obtém?

Uma régua no referencial faz um ângulo de com o eixo . Se a régua está se movendo paralelamente ao eixo do referencial com velocidade de em relação ao referencial , qual é o comprimento da régua no referencial ?

Obs.: Considere o comprimento de repouso da régua igual a .

Uma espaçonave cujo comprimento de repouso é passa por uma base espacial a uma velocidade de .

Qual é o comprimento da nave no referencial da base?

Qual é o intervalo de tempo registrado pelos tripulantes da base entre a passagem da proa e a passagem da popa da espaçonave?

O raio da Terra é e a velocidade orbital do planeta é . Suponha que a Terra passe por um observador com essa velocidade. Qual é a redução do diâmetro da Terra na direção do movimento, do ponto de vista do observador?

Uma nave espacial passa por uma base espacial com velocidade , onde é a velocidade da luz no vácuo. O comprimento da pista de pouso medido pelos funcionários da base em terra é .

Calcule o comprimento da pista no referencial do piloto da nave.

Obtenha o intervalo de tempo registrado pelo piloto entre a passagem do início e do final da pista.

Uma espaçonave da Federação de Comércio passa sobre o planeta Coruscant com velocidade de .

Uma cientista na superfície de Coruscant mede o comprimento dessa espaçonave e obtém um valor igual a .

A seguir, a espaçonave pousa na superfície de Coruscant, e a mesma cientista mede o comprimento essa espaçonave, que agora está em repouso. Qual e o valor que ela encontra?

Faça a escolha correta e a justifique. Uma nave percorre a distância entre dois países com velocidade relativística. O comandante da nave mede a distância entre as capitais dos dois países. Um cartógrafo também mediu a distância entre essas duas capitais. Qual dos observadores mediu a distância própria e qual deles mediu a menor distância?

(a ) O comandante mediu a distância própria e a menor distância.

(b ) O comandante mediu a distância própria e o cartógrafo a distância menor.

(c ) O comandante mediu a menor distância e o cartógrafo a distância própria.

(d ) O cartógrafo mediu a distância própria e a distância menor.

(e ) O comandante mediu a distância própria e ambos obtiveram o mesmo valor para a distância entre as cidades.

Uma nave espacial passa por uma base espacial com velocidade , onde é a velocidade da luz no vácuo. O comprimento da pista de pouso medido pelos funcionários da base em terra é .

Calcule o comprimento da pista no referencial do piloto da nave.

Obtenha o intervalo de tempo registrado pelo piloto entre a passagem do início e do final da pista.

Em algum momento no futuro da Terra…

Descobre-se que um asteroide, a 120 milhões de quilômetros de distância, tem sua trajetória em rota de colisão com a Terra. A velocidade do asteroide é não-relativística e para todos os efeitos práticos pode ser desprezada. A agência espacial americana manda, em t =0, uma nave não tripulada em direção ao asteroide, com velocidade (medida na Terra). Considere o sistema de referência da nave () tendo e (origem de posição e tempo coincidentes para a Terra e a nave), sendo a direção definida entre a Terra e o asteroide.

(a) De acordo ao computador de bordo da nave, já em movimento, qual é a distância que a nave deverá percorrer até chegar ao asteroide e qual será o tempo de viagem?

Uma nave espacial possui velocidade ao longo do eixo e percorre uma distância intergaláctica de anos-luz entre duas estrelas, para um dado referencial inercial. Determine a distância entre as estrelas para o referencial inercial da nave espacial.

a) anos luz.

b) anos luz.

c) anos luz.

d) anos luz.

e) anos luz.

Um triângulo retângulo está em repouso em relação a um referencial inercial e possui área . Os lados do triângulo que são ortogonais entre si possuem o mesmo comprimento , no qual um lado é paralelo ao eixo e o outro paralelo ao eixo , em relação a . O referencial se move com velocidade em relação a . Determine a área desse triângulo em relação ao referencial inercial .

a) .

b) .

c) .

d) .

Uma barra de comprimento próprio L, orientada segundo um ângulo em relação ao eixo

x está em repouso em um sistema inercial S, conforme a figura. Considere um sistema S’

que se move com velocidade constante em relação a S. Nos itens abaixo expresse

suas respostas em termos de L, , , e da velocidade da luz c.

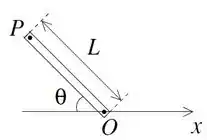
(a) Qual é o comprimento L’ da barra no sistema S’?

(b) Qual é o ângulo de orientação da barra no sistema S’?

Uma régua de comprimento de 2m está em repouso e posicionada tal que faz um ângulo de 45◦ com o eixo x do referencial inercial S. O referencial inercial S’ se move com velocidade em relação ao referencial S. Determine o comprimento da régua medido pelo referencial S’.

(a) .

(b).

(c) 2m.

(d) 3m.

(e) 2.

(f) 2

Para um dado referencial inercial, duas réguas posicionadas paralelamente ao eixo x do referencial possuem o mesmo comprimento de . A régua está parada enquanto a régua possui velocidade constante para o dado referencial inercial. Determine os comprimentos das réguas e para um outro referencial que possui velocidade constante em relação ao primeiro.

a) e .

b) e .

c) e .

d) e .

e) e .

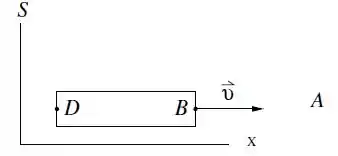
Uma espaçonave de comprimento próprio move-se com velocidade com e passa por um observador em repouso no ponto A do eixo x do sistema de coordenadas S, conforme indicado na figura. O observador registra em seu relógio um intervalo de tempo para a passagem da espaçonave por ele, isto é, o intervalo de tempo entre a passagem de B e D pelo ponto A. Calcule a velocidade expressando sua resposta somente em termos de e dos parâmetros e

Uma nave espacial com comprimento próprio de ao longo do eixo passa por uma estação transmissora com velocidade de . No instante em que a frente da nave passa pelo transmissor, dois relógios, um na frente da nave e outro no transmissor são sincronizados para . No momento em que a parte de trás da nave passa pelo transmissor, um sinal luminoso é enviado pelo transmissor e, logo depois, detectado na frente da nave.

1. No instante em que o sinal luminoso foi enviado, qual a marcação do relógio a bordo da nave?
2. No instante em que o sinal luminoso alcançou a frente da nave, qual a marcação do relógio a bordo da nave?
3. No instante em que o sinal luminoso alcançou a frente da nave, qual a marcação do relógio na estação transmissora?

Considere uma estrela situada à uma distância medida por um observador em repouso na Terra. Um astronauta parte da Terra em direção à estrela com velocidade .

Sob o ponto de vista do astronauta, qual é a distância percorrida e o tempo de viagem até a estrela?

Qual é a duração da viagem Terra-estrela medida pelo observador na Terra?

Se na metade da viagem (para o observador na Terra) o astronauta emitir um sinal de luz em direção à Terra, quanto tempo depois da partida do astronauta esse sinal será observado pelo observador na Terra?

Um dado referencial inercial observa um anel circular de raio , posicionado no plano , mover-se como um tudo com velocidade . Um outro referencial inercial observa o mesmo anel parado e posicionado no plano . A forma desse anel para o referencial é descrita por

a) Uma elipse, cujo eixo MAIOR é paralelo ao eixo .

b) Uma elipse, cujo eixo MAIOR é paralelo ao eixo .

c) Uma circunferência, cujo raio é MENOR que .

d) Uma circunferência, cujo raio é MAIOR que .

Uma espaçonave cujo comprimento em repouso vale passa por uma base espacial com velocidade de . Qual o comprimento da nave no referencial da base?

1. 130,0 m.
2. 216,7 m.
3. 78,0 m.
4. 107,2 m.
5. Não há dados suficientes para se estimar o comprimento.

Marque X na escolha correta e a justifique. Dois eventos ocorrem a 100 m de distância, separados por um intervalo de tempo de 0,60 μs. Obtenha a velocidade de um referencial no qual esses eventos ocorrem no mesmo ponto do espaço. Note que c representa a velocidade da luz.

1-( ) 0,18 c.

2-( ) 0,25 c.

3-( ) 0,56 c.

4-( ) 0,82 c.

Uma partícula elementar produzida em um experimento de laboratório percorre 0,230 mm no interior do laboratório, com uma velocidade relativa ao laboratório de 0,960 c, antes de decair em outra partícula.

(b ) Obtenha a distância percorrida pela partícula em seu referencial de repouso.

Um observador parado na Terra mede o comprimento de uma nave espacial em movimento e encontra o valor de . Sabendo que a velocidade da nave em relação à Terra é de , o comprimento da nave, para um observador dentro da nave, será?

a) .

b) .

c) .

d) .

Um relógio se move com velocidade constante em relação a um referencial inercial. Após se passar 2 horas para o referencial inercial, o relógio acusa que o tempo transcorrido foi de horas. A velocidade do relógio em relação ao referencial inercial é dada por

a) .

b) .

c) .

d) .

e) .

Uma barra de comprimento próprio move-se com velocidade constante relativamente ao sistema conforme a figura.

A extremidade da barra passa pela origem de no instante . Nesse instante é emitido de um sinal de luz que viaja de para .

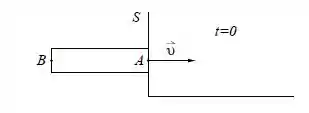
1. Em que instante medido num referencial em repouso em relação à barra o sinal chega a ?
2. Em que instante medido no referencial o sinal chega a ?

Um observador parado em relação a um referencial inercial mede o comprimento de um buraco no chão, em repouso em relação ao dado referencial, e obtém o valor de .

O observador também mede o comprimento de uma nave espacial que está em movimento retilíneo uniforme em relação ao referencial inercial, obtendo o valor de .

Qual deve ser a velocidade da nave em relação à pessoa para que a nave tenha o mesmo comprimento do buraco, do ponto de vista de um passageiro em repouso em relação à nave? Considere que os comprimentos da nave e do buraco sejam paralelos à velocidade da nave.

5. O comprimento do buraco é sempre maior que o comprimento da nave para os passageiros.

Uma nave espacial realiza uma viagem intergaláctica entre duas estrelas que estão em repouso, para um dado referencial inercial.

Um cronômetro marca o intervalo de tempo de anos para completar a viagem, enquanto um medidor de kilometragem, ambos presos e parados em relação à nave, marca o valor total de anos-luz.

Considerando a velocidade da nave em relação ao referencial inercial constante, determine o valor dessa velocidade.

Uma espaçonave de comprimento próprio move-se com velocidade em relação ao sistema inercial . De acordo com um observador em repouso em a espaçonave leva um intervalo de tempo igual a para passar pela origem de , conforme a figura.

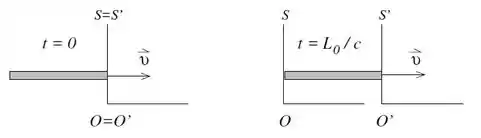
1. Calcule o módulo da velocidade da espaçonave em termos de
2. Calcule o intervalo de tempo para a passagem da espaçonave pela origem no referencial da espaçonave.