Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Fator de Lorentz

Ver Todos os Exercícios

Teoria

O fator de Lorentz é uma equação muito utilizada nas equações da relatividade! Bora conhecer melhor ele?!

📢 Clique para ver mais:

Fator de Velocidade

O Fator de Velocidade , também conhecido como parâmetro de velocidade é definido por:

Onde é a velocidade relativa entre dois referenciais e c é a velocidade da luz, que vale aproximadamente .

Vamos entender o parâmetro de velocidade fazendo um exemplo, considere um caminhão de uma empresa de entregas que nunca atrasa uma entrega sequer.

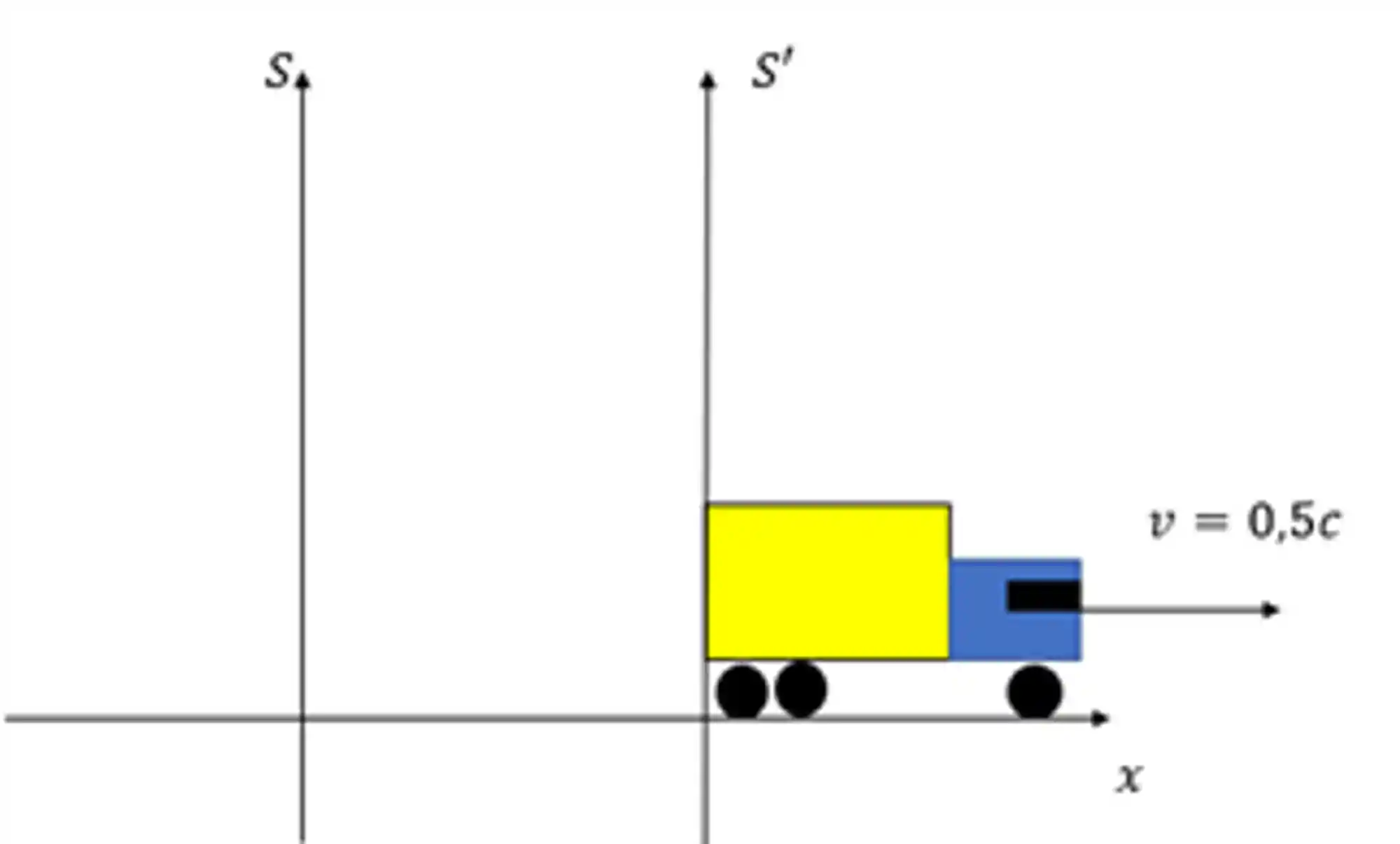
Fator de velocidade: Exemplo
Fator de velocidade: Exemplo

O caminhão se move com velocidade igual a metade da velocidade da luz, qual seria o parâmetro de velocidade desse caminhão??

Podemos dizer que:

Substituindo no parâmetro de velocidade, temos:

Como nenhuma velocidade pode ser superior a da luz portanto, então .

Fórmula do Fator de Lorentz

O Fator de Lorentz é definido por:

E como nunca é menor que , a gente pode dizer que . E se a gente quiser descobrir o valor do fator de Lorentz pro exemplo acima basta substituir o parâmetro de velocidade aqui:

E com isso se a gente analisar as equações da relatividade e podemos tirar as seguintes conclusões:

Como o tempo nunca vai se contrair, sempre vai se dilatar pro observador no referencial fixo que vê alguém se movimentando em .

No caso do caminhão a gente terá:

Como , o comprimento nunca se dilata, sempre vai se contrair pro observador no referencial fixo que observa um movimento em .

Transformações de Lorentz

As transformações de Lorentz descrevem como, de acordo com a relatividade especial, as medidas de espaço e tempo de dois observadores se alteram em cada sistema de referência.

Pra aprender mais sobre as Transformações de Lorentz confira o vídeo abaixo:

Agora vamos praticar com exercícios!

Fórmula do Fator de Lorentz

Transformações de Lorentz

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 178-21.

Um relógio está se movendo ao longo do eixo x com uma velocidade de 0,6 c e indica o instante t = 0 ao passar pela origem.

a Calcule o fator de Lorentz do relógio.

b Qual é a leitura do relógio ao passar pelo ponto x = 180 m ?

Passo 1

a Calcule o fator de Lorentz do relógio.

O fator de Lorentz é dado por:

γ = 1 1 - u 2 c 2

Onde u = 0,6 c , logo:

γ = 1 1 - 0,6 c c 2

γ = 1,25

Passo 2

b Qual é a leitura do relógio ao passar pelo ponto x = 180 m ?

O tempo medido do referencial em repouso é dado por:

Δ t = x u = 180 0,6 × 3 × 10 8

Δ t = 1 × 10 - 6 s

Utilizando a equação de dilatação do tempo, teremos:

Δ t = γ Δ t 0 → Δ t 0 = Δ t γ

Portanto:

Δ t 0 = 1 × 10 - 6 1,25

Δ t 0 = 8,0 × 10 - 7 s

Resposta

a

γ = 1,25

b

Δ t 0 = 8,0 × 10 - 7 s

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 177-8.

O comprimento de uma espaçonave em um certo referencial é a metade do comprimento de repouso. a Com três algarismos significativos, qual é o parâmetro de velocidade β da espaçonave no referencial do observador? b Qual é a relação entre a rapidez da passagem do tempo no referencial da nave e no referencial do observador?

Passo 1

a Com três algarismos significativos, qual é o parâmetro de velocidade β da espaçonave no referencial do observador?

Através da equação de contração do comprimento, temos que:

l = l 0 γ

De acordo com o enunciado, l = l 0 / 2 , logo:

l 0 2 = l 0 γ

γ = 2

Onde:

γ = 1 1 - β 2

Logo:

1 1 - β 2 = 2

1 1 - β 2 = 4

β = 1 - 1 4

β = 0,866

Passo 2

b Qual é a relação entre a rapidez da passagem do tempo no referencial da nave e no referencial do observador?

A passagem do tempo Δ t 0 no referencial da nave e a passagem do tempo Δ t no referencial do observador estão relacionadas por:

Δ t = γ Δ t 0

Assim, as duas estão relacionadas pelo fator de Lorentz, dado por:

γ = 2

Resposta

a

β = 0,866

b

As duas estão relacionadas pelo fator de Lorentz, onde γ = 2 .

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 177-12.

Uma barra se move com velocidade constante v ao longo do eixo x do referencial S , com a maior dimensão da barra paralela ao eixo x . Um observador estacionário no referencial S mede o comprimento L da barra.

A figura abaixo mostra o valor de L em função do parâmetro de velocidade β para 0 ≤ β ≤ 0,8 . A escala do eixo vertical é definida por L a = 1,0 m . Qual é o valor de L para u = 0,95 c ?

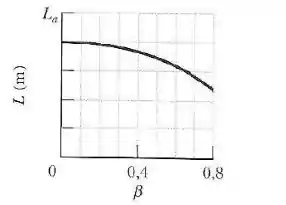
Passo 1

A partir da escala dada pelo problema, quando β = 0 , ou seja, u = 0 (referencial em repouso), o comprimento da barra vale 0,8 m .

Logo:

L 0 = 0,8 m

Agora podemos usar a equação de contração do comprimento pra simplificar a nossa vida:

L = L 0 1 - u 2 c 2

Substituindo os valores, teremos:

L = 0,8 1 - 0,95 c c 2

L = 0,25 m

Resposta

L = 0,25 m

Exercício Resolvido #4

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 177-4.

O referencial S ' passa pelo referencial S a uma velocidade v ao longo da direção comum dos eixos x ' e x , como na figura abaixo.

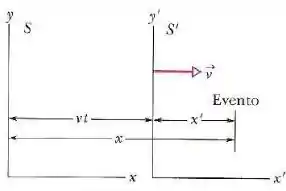
Um observador estacionário no referencial S ' mede um certo intervalo de tempo com seu relógio de pulso. Um observador estacionário no referencial S mede o intervalo correspondente Δ t .

A figura abaixo mostra a variação de Δ t com o parâmetro de velocidade β no intervalo 0 ≤ β ≤ 0,8 . A escala do eixo vertical é definida por Δ t a = 14,0 s . Qual é o valor de Δ t para u = 0,98 c ?

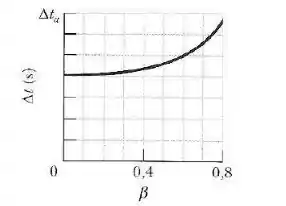
Passo 1

A partir da escala dada pelo problema, quando β = 0 , ou seja, u = 0 (referencial em repouso), o intervalo de tempo vale 8,0 s .

Logo:

Δ t 0 = 8,0 s

Agora podemos usar a equação de dilatação do tempo para resolver o problema:

Δ t = Δ t 0 1 - u 2 c 2

Substituindo os valores, teremos:

Δ t = 8 1 - 0,98 c c 2

Δ t = 40 s

Resposta

Δ t = 40 s

Exercício Resolvido #5

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 177-6.

De volta para o futuro. Suponha que um astronauta é 20 anos mais velho que a filha. Depois de passar 4000 anos (no seu referencial) viajando pelo universo com velocidade constante, em uma viagem de ida e volta, descobre, ao chegar à Terra, que está 20 anos mais moço que a filha.

Determine o parâmetro de velocidade β da nave do astronauta em relação à Terra.

Passo 1

O astronauta sai da Terra 20 anos mais velho que a filha e volta 20 anos mais moço. Sendo assim, se para o astronauta se passaram 4000 anos, para a sua filha se passaram 4040 anos, certo?

Assim, como o tempo próprio é o tempo medido pelo astronauta, temos que:

Δ t 0 = 4000   a n o s

Δ t = 4040   a n o s

Usando a equação de dilatação do tempo, temos que:

Δ t = γ Δ t 0

γ = Δ t Δ t 0

Substituindo os valores, teremos:

γ = 4040 4000

γ = 1,01

Passo 2

O fator de Lorentz γ está relacionado com o parâmetro de velocidade β da seguinte forma:

γ = 1 1 - β 2

Isolando o β , teremos:

β = 1 - 1 γ 2

Agora é substituir os valores e partir pro abraço.

β = 1 - 1 1,01 2

β = 0,14

Resposta

β = 0,14

Exercício Resolvido #6

Elaboração própria

Uma espaçonave viaja com velocidade 0,8 c e o objetivo é concluir um percurso de 10000 k m .

a Calcule o parâmetro de velocidade e o fator de Lorentz da nave.

b Qual é o tempo medido para um observador na nave ao completar o percurso?

c Qual é o tempo medido para um observador fixo fora da nave?

Passo 1

Para o item a, vamos começar calculando o Parâmetro de velocidade.

Com u = 0,8 c temos:

β = u c = 0,8

Agora podemos calcular o fator de Lorentz que é dado por:

γ = 1 1 - β 2

E com o β calculado e substituido na equação temos.

γ = 1 1 - 0,64

γ = 5 3

Passo 2

O item b, pede o tempo medido pelo observador na nave. Para ele o tempo observado não sofre distorção pois é o tempo próprio ∆ t 0 .

O tempo medido do referencial em repouso é dado por:

∆ t 0 . = ∆ x u = 10000 × 10 3 0 , 8 × 3 × 10 8

Δ t 0 = 0,04167 s = 41,67 m s

Passo 3

Para o item c, o enunciado pede o tempo medido por um observador fixo e para ele ocorre a dilatação do tempo.

Utilizando a equação de dilatação do tempo, teremos:

Δ t = γ Δ t 0 →

Portanto:

Δ t = 41,67 × 5 3

Δ t = 69,45 m s

Resposta

a

β = 0,8

γ = 5 3

b

Δ t 0 = 41,67 m s

c Δ t = 69,45 m s

Exercícios de Livros Relacionados

51. As naves da Federação Solar são marcadas com o símbolo da Federação, um círculo, enquanto as naves do Império Denebian são marcadas com o símbolo do Império, uma elipse cujo o eixo maior é 1,40 ve
1 03 . Determine o parâmetro de velocidade para as seguintes velocidades: ( a ) o deslocamento de uma placa tectônica típica ( 2,5c m / a n o ) ; ( b ) a velocidade de deriva dos elétrons em um condut
O píon neutro π 0 tem uma massa de repouso de 135,0 MeV / c2. Esta partícula pode ser criada em uma colisão próton-próton: p + p → p + p + π0. Determine o limiar de energia cinética para a criação de
Use a equação de expansão binomial 1 + x n = 1 + n x + n ( n - 1 ) 2 x 2 + … ≈ 1 + n x , x ≪ 1 para derivar os seguintes resultados para o caso em que v é muito menor que c, e use os resultados quando
Uma espaçonave interestelar viaja da Terra para um sistema estelar a 12 anos-luz de distância (conforme medido no referencial da Terra). A viagem dura 15 anos, conforme medido pelos relógios da nave.