Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Energia Interna de um Gás

Ver Todos os Exercícios

Teoria

A energia interna de um gás é igual a soma das energias cinéticas das partículas que constituem esse gás. Bora entender melhor como isso tudo funciona?!


📢 Clique para ver mais:

Como Calcular a Energia Interna de um Gás

Acabamos de ver que existe uma energia interna do gás devido à energia cinética de suas moléculas. Podemos então escrever:

Onde é a energia cinética média de cada molécula do gás. Quanto maior for a agitação das moléculas maior é temperatura e também a sua energia cinética e consequentemente sua energia interna. Ou seja, a energia interna do gás depende diretamente da sua temperatura .

Gases Monoatômicos

Para calcular a energia interna de gases monoatômicos usamos a seguinte fórmula:

Onde é o número de mols, é a constante dos gases ideais e é a variação de temperatura.

Gases Diatômicos

Para gases diatômicos a fórmula para calcular a energia interna do gás não muda muito, olha só:

Beleza, mas… qual é a lógica dessas fórmulas? Porque tem um na fórmula do gás monoatômico e um no gás diatômico? Bora entender?

Gases Poliatômicos

Agora a gente vai finalmente pro caso geral! Para calcular a energia interna de qualquer molécula, usamos a seguinte fórmula:

Onde é o grau de liberdade da molécula. O grau de liberdade de uma molécula é relacionada ao tipo de molécula do gás, se ela é monoatômica, diatômica ou poliatômica. Dependendo da geometria da molécula, podemos ter velocidades e velocidades angulares em algumas direções:

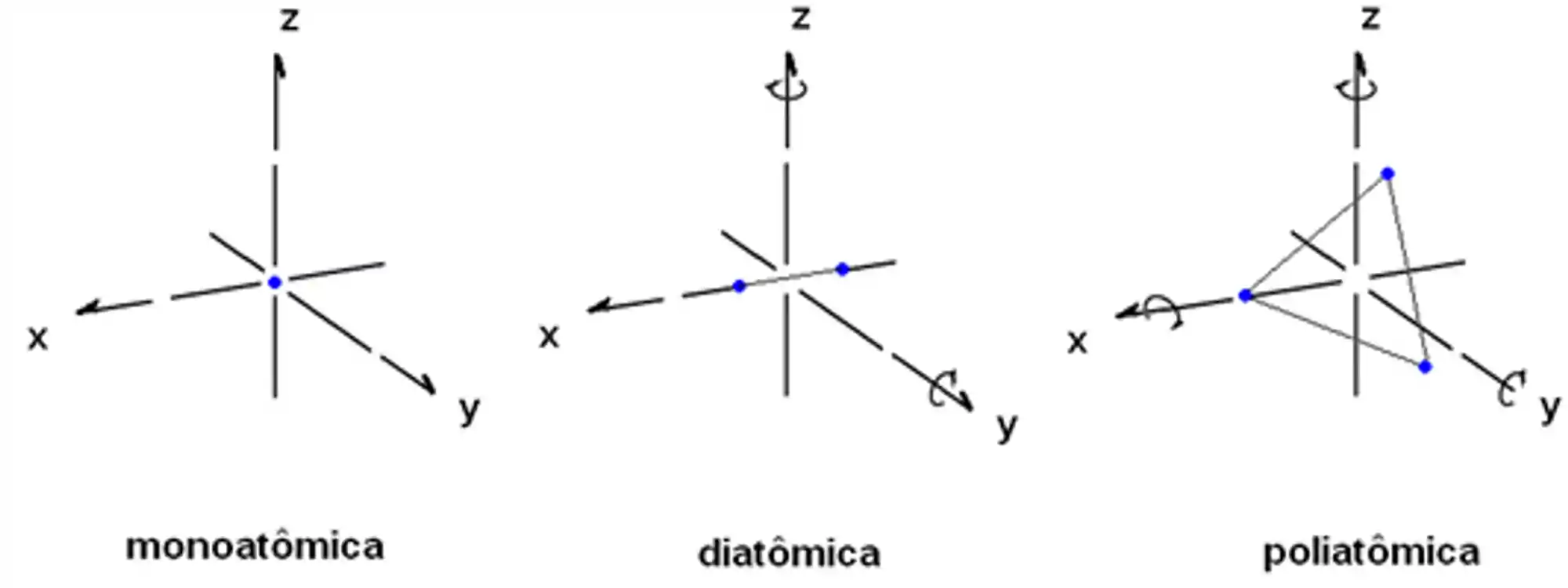
Graus de liberdade de moléculas monoatômicas, diatômicas e poliatômicas.
Graus de liberdade de moléculas monoatômicas, diatômicas e poliatômicas.

Na molécula monoatômica, temos apenas 3 graus de liberdade: translação nos eixos , e . Na molécula diatômica, além dos 3 graus de liberdade de translação, temos mais 2 graus de liberdade de rotação, nos eixos e . Note que, no eixo x, a rotação não altera a molécula, pois estamos considerando que ela é uma reta.


E na molécula poliatômica, temos os 3 graus de liberdade de translação e 3 graus de liberdade de rotação. Então podemos colocar isso numa tabela:

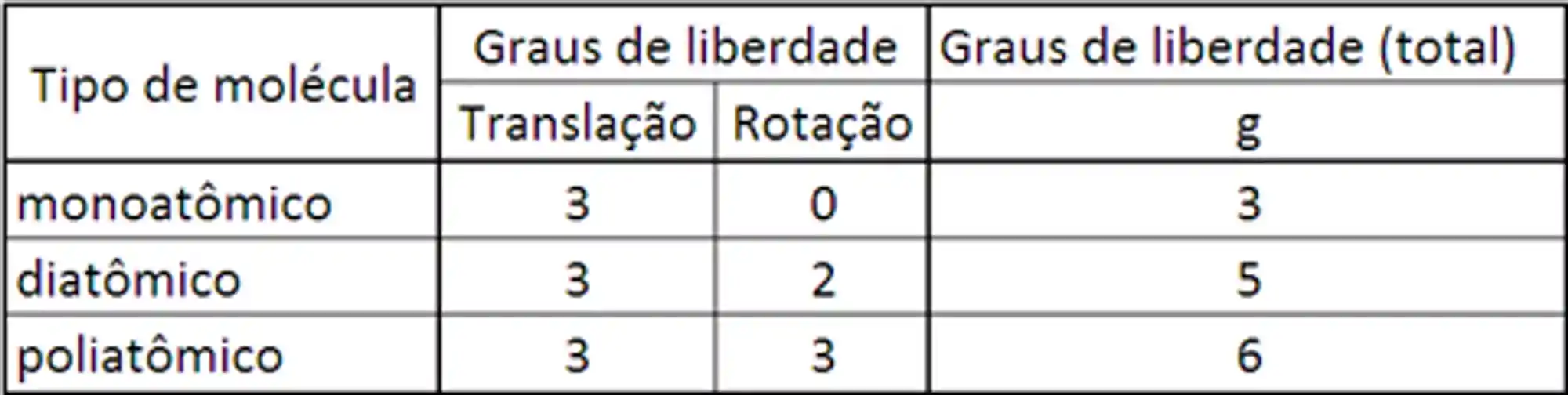
Tabela de graus de liberdade para o cálculo da energia interna de uma molécula gasosa
Tabela de graus de liberdade para o cálculo da energia interna de uma molécula gasosa

Você também pode conferir esse conteúdo em vídeo:

Sinal e Sentido da Energia Interna

A variação de energia interna entre dois pontos não depende do caminho, mas o seu sentido pode mudar:

Esse sentido é definido pela variação da temperatura, positivo se e negativo se .

Calor Específico Molar

A quantidade de calor pode ser calculado por:

Onde é a massa, é o calor específico. O problema é que essa fórmula só serve para líquidos, quando estamos falando de gases ideais o calor específico vai variar.

Temos dois valores diferentes para calor específico de gases ideais. Um a pressão constante e outro a volume constante . Dessa forma podemos calcular a quantidade de calor da seguinte forma:

O calor específico a volume constante e a pressão constante pode se relacionar a partir da seguinte fórmula:

Onde é a constante universal dos gases. Em uma mistura de gases usamos:

Agora vamos praticar com exercícios?

Calor Específico Molar

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 . Rio de Janeiro: LTC , 2008, x-y 47

A figura representa a energia térmica de 0,14   m o l de gás em função da temperatura.

Quanto vale c v para este gás?

Passo 1

Para determinar o calor específico à volume constante do gás em questão, precisamos lembrar da seguinte relação:

Δ U = n . c v . Δ T

Pelo gráfico, podemos obter as seguintes informações:

Δ U = 1892 - 1092 = 800   J

Sabemos que a variação de temperatura em Celsius é igual à variação de temperatura em Kelvin. Então, não precisamos transformar! Logo:

Δ T = 200 - 0 = 200   K

Substituindo na equação, temos:

Δ U = n . c v . Δ T

800 = 0,14 . c v . 200

c v = 28,6   J / m o l . K

Resposta

c v = 28,6   J / m o l . K

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 243-50

Fornecemos 70 J de calor a um mol de gás diatômico, que se expande a pressão constante. As moléculas do gás giram, mas não oscilam. De quanto a energia interna do gás aumenta?

Passo 1

Bom, galera, vamos prestar primeiro atenção nisso: “As moléculas do gás giram, mas não oscilam”. Isso que dizer o que? Quer dizer que as moléculas do gás têm os 5 graus de liberdade que vimos na teoria. Se elas também tivessem oscilação, elas teriam mais graus de liberdade.

Como elas seguem a teoria, podemos escrever:

c v = g 2 . R = 5 2 . R

c p = c v + R = 7 2 . R

Passo 2

Vamos agora prestar atenção nisso: “Fornecemos 70 J de calor a um gás diatômico, que se expande a pressão constante”. Isso quer dizer que podemos escrever:

Q = n c p ∆ T

Sendo Q o calor fornecido. Agora podemos achar o ∆ T , que vai nos ajudar a calcular a variação da energia interna:

70 = 1 . 7 R 2 . ∆ T   → 20 R = ∆ T

Passo 3

Agora vamos calcular a variação da energia interna. Vamos usar a expressão:

∆ U = g 2 n R ∆ T

Sendo g = 5 , o número de graus de liberdade, n = 1 e ∆ T = 20 R :

∆ U = 5 2 . 1 . R . 20 R

Δ U = 50   J

Resposta

∆ U = 50   J

Exercício Resolvido #3

UFRJ – 1ª Prova – 2013.2

Um pesquisador quer estudar o comportamento termodinâmico de sólidos através de uma simulação de computador.

Ele modela um sólido como uma rede cristalina de N = 1   b i l h ã o de átomos ligados aos seus vizinhos por molas ideais.

Contudo, seus “átomos” estão restritos a um plano (ou seja, a simulação é inteiramente bidimensional).

Para testar se sua simulação está bem feita, ele calcula a energia interna do seu sólido.

Qual o valor que ele espera encontrar?

a   E i n t = 1 / 2 N k B T

b   E i n t = N k B T

c   E i n t = 3 / 2 N k B T

d   E i n t = 2 N k B T

e   E i n t = 5 / 2 N k B T

f   E i n t = 3 N k B T

g E i n t = 7 / 2 N k B T

Passo 1

Queremos calcular a energia interna de N átomos.

Porém a fórmula que temos é para mols de átomos

U = g 2 . n . R . T

Temos que

k B = R / N a

E que

N = n . N a

Então substituindo na nossa fórmula chegamos em

⇒ U = g 2 N k B T

Então, só precisamos determinar quantos graus de liberdade tem cada átomo desse sólido que o problema nos falou.

Passo 2

Como a simulação é inteira bidimensional, significa que os átomos só podem vibrar em duas direções x e y . Como cada modo de vibração tem duas contribuições, a cinética e a potencial. Temos então 2 × 2 = 4 graus de liberdade.

Então

U = 4 2 N k B T

U = 2 . N . k B . T

Resposta

d

Exercício Resolvido #4

UFRJ – 1ª Prova – 2014.1

Dois gases ideais, um monoatômico e um diatômico, sofrem a mesma variação de energia interna. Marque a alternativa verdadeira.

a   A variação de temperatura, nos dois casos, é a mesma.

b   A variação de temperatura é maior no gás monoatômico.

c   A variação de temperatura é maior no gás diatômico.

d   Não é possível relacionar as variações de temperatura pois não sabemos se o sitema realiza ou não trabalho durante tal processo.

e   As temperaturas não variam.

Passo 1

Sabemos que a variação de energia interna é dada por

Δ U = g 2 n R Δ T

Supondo que os gases tem o mesmo número de mols, vamos comparar as energias internas do gás monoatômico e do gás diatômico.

No gás monoatômico, temos g = 3 (três graus de liberdade).

No gás diatômico, temos g = 5 (cinco graus de liberdade).

Passo 2

Variação de energia interna do gás monoatômico:

Δ U 1 = 3 2 n R Δ T 1

Variação de energia interna do gás diatômico:

Δ U 2 = 5 2 n R Δ T 2

Passo 3

Como a variação de energia interna é a mesma:

Δ U 1 = Δ U 2

3 2 n R Δ T 1 = 5 2 n R Δ T 2

Simplificando:

3 Δ T 1 = 5 Δ T 2

Logo:

Δ T 1 = 5 3 Δ T 2

Então:

Δ T 1 > Δ T 2

Logo: a variação de temperatura é maior no gás monoatômico!

Alternativa b .

Resposta

Alternativa b .

Exercício Resolvido #5

UFRJ – 1ª Prova – 2014.1

Como se altera a energia cinética média de um gás monoatômico ideal quando:

A pressão é duplicada a volume constante?

O volume é duplicado a pressão constante?

a   Permanece inalterada em ambos os casos.

b   Cai à metade em ambos os casos.

c   Dobra em ambos os casos.

d   Quadruplica e cai a 1 / 4 , respectivamente.

e   Dobra e cai à metade, respectivamente.

Passo 1

A energia cinética média de n   m o l s de um gás é dada por:

E c m = g 2 n R T

onde g é o número de graus de liberdade do gás.

Vamos analisar como a energia cinética muda nos dois casos.

Passo 2

Pressão é duplicada a volume constante:

Vamos considerar que o gás está, inicialmente, a uma pressão p 1 , volume V 1 e temperatura T 1 .

Então, sua energia cinética média é dada por:

E 1 = g 2 n R T 1

Quando a pressão é duplicada a volume constante, temos que descobrir qual vai ser a nova temperatura, para podermos calcular a energia cinética média E 2 .

Pela equação dos gases ideais:

p 1 V 1 T 1 = p 2 V 2 T 2

Como a pressão dobra: p 2 = 2 p 1

E como isso ocorre a volume constante: V 1 = V 2

Logo:

p 1 V 1 T 1 = 2 p 1 V 1 T 2

⇒ 1 T 1 = 2 T 2

⇒ T 2 = 2 T 1

A nova energia cinética média será:

E 2 = g 2 n R T 2

⇒ E 2 = g 2 n R 2 T 1

⇒ E 2 = 2 g 2 n R T 1

Logo:

E 2 = 2 E 1

Então a energia cinética média dobrou.

Só nos resta as alternativas ( c ) ou ( e ) .

Passo 3

Usando o mesmo raciocínio para o outro caso, temos que:

A pressão é constante: p 1 = p 2

O volume dobra: V 2 = 2 V 1

Equação dos gases ideais:

p 1 V 1 T 1 = p 2 V 2 T 2

⇒ p 1 V 1 T 1 = p 1 2 V 1 T 2

⇒ T 2 = 2 T 1

Como a temperatura dobrou, a energia cinética média também dobra.

Então, nesse caso, a energia cinética média também dobra!

Logo, alternativa c .

Resposta

Alternativa c .

Exercícios de Livros Relacionados

O invólucro e a cesta de um balão de ar quente têm um peso total de 2,454k N e o invólucro tem uma capacidade (volume) de 2,18.10 3m 3 . Qual deve ser a temperatura do ar no interior do invólucro, qua
Um recipiente contém uma mistura de três gases não reagentes: 2,40 mol do gás 1 com C V 1 = 12,0J / m o l . K , 1,50m o l do gás 2 com C V 2 = 12,8J / m o l . K e 3,20m o l do gás 3 com C V 3 = 20,0J
A temperatura de 2,00m o l s de um gás ideal monoatômico é aumentada de 15,0K a volume constante. Determine (a) o trabalho W realizado pelo gás, (b) a quantidade Q de calor transferida para o gás, (c)
A massa da molécula de um gás pode ser calculada a partir do calor específico a volume constante c V . (Note que não se trata de C V ) Tome c V = 0,075c a l / g ° C para o argônio e calcule (a) a mass
Fornecemos 70J de calor a um gás diatômico, que se expande a pressão constante. As moléculas do gás giram, mas não oscilam. De quanto a energia interna do gás aumenta?