Se aumentarmos em o raio e a altura de um cone equilátero, em quantos por cento seu volume será aumentado?
Passo 1
Primeiro, vamos tentar entender o que ele quer. Repara que tínhamos um cone equilátero, aumentamos o seu raio e a altura, ele quer saber como vai ficar o volume.
Isso nos diz que temos que achar o volume do cone equilátero antes e depois desse aumento.
Lembrando que, o volume do cone é
Precisamos variar o raio e a altura aqui. Antes, vamos entender o que é um cone equilátero.
Quando olhamos um cone de frente, vemos um triângulo certo? Dá uma olhada nessa figura aqui
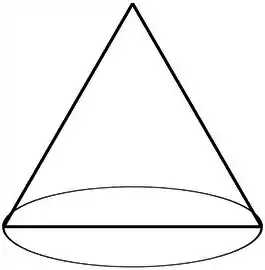
Esse é o nosso cone. O cone equilátero, é o cone que esse triângulo é um triângulo equilátero.
Assim, vamos ter
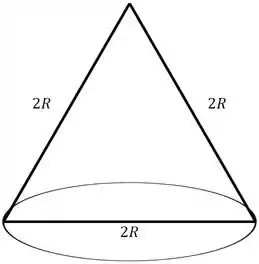
Passo 2
Beleza, agora precisamos achar o novo volume. Repara que vamos ter
E
Vamos passar essa porcentagem para decimal. Vamos ter
E
O novo volume vai ser
Trocando os valores do raio e da altura.
Passo 3
Agora temos que comparar o novo volume com o volume anterior. Repara que temos
Assim, vamos ter
Isso nos diz que
Repara que isso representa um aumento de no volume.
Resposta
aumento de no volume