Considere um cubo cuja aresta vale e uma esfera interna ao cubo, e que tangencia as faces desse cubo.
Determine o volume interno do cubo que é externo à esfera.
Passo 1
Repara que o que ele quer é o volume interno do cubo e externo à esfera. Isso nada mais é que o volume do cubo, menos o volume da esfera. Vai ser a parte entre a esfera e o cubo.
Vamos chamar de esse volume, então:
Passo 2
Vamos começar achando o volume do cubo. Para isso, é só pegar a aresta do cubo e elevá-la a . Então
Passo 3
Agora precisamos do volume da esfera. Para isso, vamos usar a fórmula do volume da esfera.
Opa, mas precisamos do raio da esfera. E agora? Ele deu uma relação entre a esfera e o cubo. A esfera é interna ao cubo, e tangencia as duas faces. Vamos ver uma figura disso.
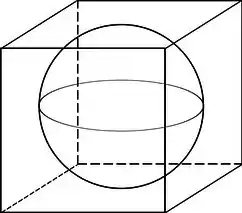
Repara que a altura do cubo, é igual ao diâmetro da esfera. Assim, vamos ter
E agora temos o raio em função daquele que ele deu no início.
Voltando para o volume da esfera, temos
Passo 4
Agora que achamos o volume do cubo e da esfera, podemos achar o volume que ele pediu.
Vamos ter
Aqui não temos muito o que fazer. Vamos deixar assim mesmo, e essa é nossa resposta