Considere uma folha de papel cujo perímetro é e um dos lados é o dobro do outro. A partir da união de duas arestas dessa folha se forma um cilindro. Determine o volume do cilindro com a maior área de base.
Passo 1
Temos uma folha de papel, vamos fazer o seu desenho

Não sabemos nem o a base nem a altura desse retângulo, mas ele disse que um dos lados é o dobro do outro. Assim, vamos ter
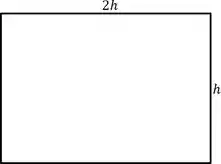
Além disso, conseguimos achar esse tranquilamente. Ele disse que o perímetro é .
Assim
Passo 2
Para fazer o cilindro, temos que “enrolar” essa folha. O detalhe é em qual direção vamos enrolar essa folha. Repara que vamos ter
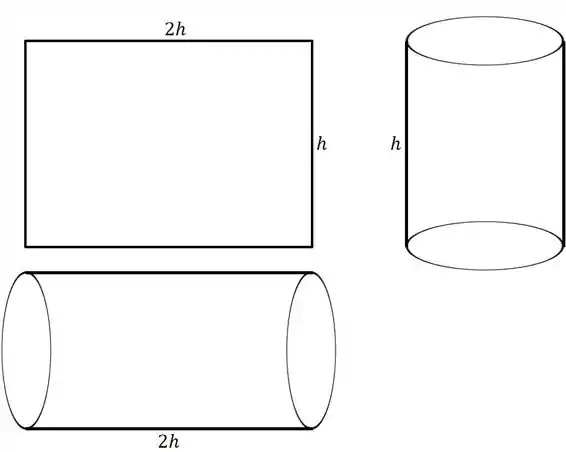
Eu desenhei ali as duas direções que eu posso rodar. Essa direção vai definir quem é a altura.
Ele quer o volume de um desses cilindros, mas qual?
Repara que ele falou o que tem maior área da base, então precisamos ver qual a área de cada uma dessas bases.
Passo 3
As duas bases são círculos. Para saber qual maior área, basta pegar a que tiver maior raio.
Então basta achar o raio da base de cada um desse cilindros.
Vamos começar com o seguinte cilindro
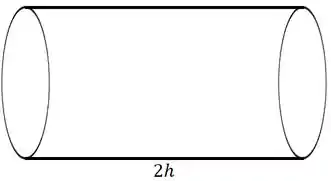
Repara que a altura se manteve como o comprimento da folha, enquanto o comprimento da base do cilindro vai ser igual à altura da folha.
Vamos chamar de o raio da base desse cilindro.
Assim, vamos ter
Trocando o valor de que achamos no passo
Passo 4
Vamos agora para o outro cilindro
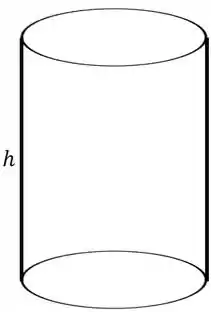
Repara que a altura se manteve como a altura da folha, enquanto o comprimento da base do cilindro vai ser igual ao comprimento da folha.
Vamos chamar de o raio da base desse cilindro.
Assim, vamos ter
Trocando o valor de que achamos no passo
Repara que esse raio, vai ser maior que o outro. Isso porque é maior que
Passo 5
Vamos ao volume desse segundo cilindro então.
Ele vai ser
Trocando o valor do raio e de , vamos ter