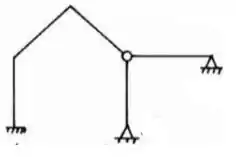
Determine o número de hiperestáticos externos e internos da estrutura abaixo.
Passo 1
Sabemos que precisamos seguir algumas regrinhas se quisermos determinar o número de hiperestáticos da nossa estrutura aí em cima, então vamos lá:
- Hiperestáticos externos
- Hiperestáticos internos
- Hiperestáticos totais
Sabemos que para determinar o número de hiperestáticos externos precisamos saber a diferença entre o número de incógnitas e o número de equações. Começando pelas incógnitas temos: 2 apoios do segundo gênero, e um apoio do primeiro gênero.


Com isso totaliza-se 7 incógnitas no problema.
Sabemos que o número de equações pode ser definidos por dois grupos. Primeiro as nossas velhas amigas equações de equilíbrio.
E como temos uma rótula em que chegam 3 barras devemos seguir o seguinte passo:
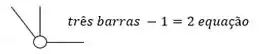
Isso totaliza 5 equações.
Ou seja, 2 hiperestáticos externos.
Passo 2
Sabemos que para determinar o número de hiperestáticos internos precisamos saber a o número de regiões fechadas, que no nosso problema não existe. Logo o número de hiperestáticos internos é zero.
Passo 3
Por fim, determinamos o total de hiperestáticos.