Determine o número de hiperestáticos externos, internos e total da estrutura abaixo.
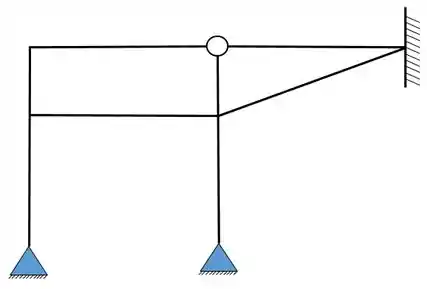
Passo 1
Fala, pessoal, vamos resolver esse problema de hiperestática?
A gente vai separar cada etapa sendo a primeira para achar o número de hiperestáticos externos, a segunda o número de hiperestáticos internos e a última a soma dos dois que é o total.
Então partiu!!
Passo 2
- Hiperestáticos externos
- Hiperestáticos internos
- Hiperestáticos totais
Para determinar o número de hiperestáticos externos precisamos saber a diferença entre o número de incógnitas e o número de equações.
Começando pelas incógnitas temos: 2 do segundo gênero e 1 apoio do terceiro gênero. Sendo assim vamos utilizar a nossa tabelinha para achar o número de incógnitas:

Portanto, o número total de incógnitas será de:
Com isso temos um total de 7 incógnitas.
Agora vamos achar o número de equações. Isso vai depender das três equações da estática (para o caso bidimensional) mais as equações das rótulas.
Sabemos que o número de equações pode ser definidos por dois grupos. Primeiro as nossas velhas amigas equações de equilíbrio.
E como temos uma rótula, vamos ter as nossas 3 velhas amigas equações de equilíbrio mais o equivalente da rótula. Vamos lembrar como fazer o cálculo para a rótula:
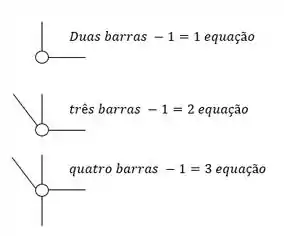
Como no problema temos uma rótula ligada a três barras vamos ter 2 equações a mais. Totalizando 5 equações.
Ou seja, há 5 hiperestáticos externos.
Passo 3
Sabemos que para determinar o número de hiperestáticos internos precisamos saber a o número de regiões fechadas.
No nosso problema temos 2 regiões fechadas
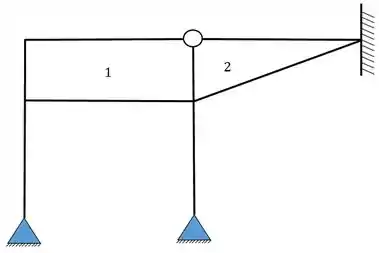
Logo nós vamos ter:
Passo 4
Por fim, determinamos o total de hiperestáticos.