P2 de Física 1 da UFRJ - 2012.1

Uma granada está em repouso sobre uma mesa horizontal e sem atrito. Num dado instante ela explode em dois fragmentos de massas e velocidades diferentes, onde os fragmentos permanecem movimentando-se sobre a mesa. É possível afirmar que:

1. A energia cinética é conservada.
2. A posição do centro de massa das partículas varia com o tempo.
3. O momento linear total do sistema não é conservado.
4. A velocidade do centro de massa é nula após a explosão.
5. Nenhuma das opções acima está correta.

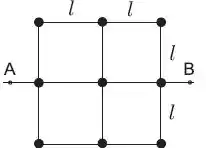
Considere um corpo rígido constituído por: hastes finas, rígidas, de massa desprezível e de comprimento e um conjunto de nove massas iguais a (que podem ser consideradas puntiformes) conforme a figura abaixo. O momento de inércia desse conjunto em torno do eixo é dado por:

Uma partícula de momento , projétil, colide não frontalmente, isto é, colide bidimensionalmente, com uma outra partícula, inicialmente em repouso, que chamamos de alvo. Após a colisão o projétil tem momento e o alvo sai com momento . A conservação do momento linear, neste processo é corretamente representado pelo diagrama:

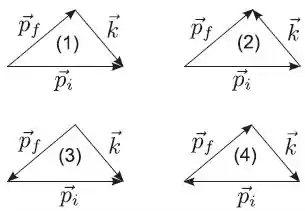
5. Nenhum diagrama está correto

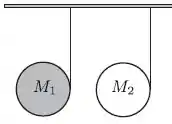
Dois discos de mesmo raio e de massa diferentes, onde , estão presos ao teto por fios ideais e enrolados em suas bordas. Liberados a partir do repouso eles caem verticalmente onde é o módulo da aceleração local da gravidade; o momento de inércia de um disco em torno do seu eixo de rotação que passa pelo seu centro é igual . Os módulos das trações nos fios em cada disco são e e as acelerações dos seus centros de massa são e , respectivamente, a opção correta abaixo é:

2. ;
5. e

Um arame homogêneo e uniforme, de espessura desprezível, é moldado na forma de um quadrado de aresta Retira-se então um segmento de comprimento de duas arestas , reduzindo-as à metade, como mostra a figura. No novo sistema a distancia do centro de massa à origem é igual a,

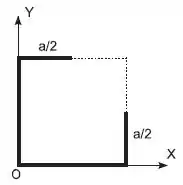
Considere uma partícula de massa presa ao teto em um suporte fixo por meio de um fio ideal de comprimento , formando um pêndulo. A partícula é solta a partir do repouso, com o fio esticado, a uma distância do teto; é o módulo da aceleração local da gravidade. Qual é o módulo do momento angular da partícula com relação ao ponto de sustentação do fio quando ela passa pelo ponto mais baixo da trajetória?

Uma esfera de raio e massa rola sem deslizar sobre uma mesa horizontal com velocidade angular constante. Sabendo-se que o momento de inércia de uma esfera segundo um eixo que passa pelo seu centro é , a energia cinética desta esfera é:

Considere um sistema formado por uma partícula e por uma mola ideal, conforme a figura. A partícula pode mover-se sobre uma mesa horizontal lisa sob a ação da força da mola, cuja outra extremidade está presa à mesa. É correto afirmar que:

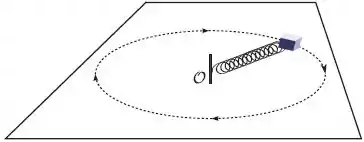
1. O momento angular não se conserva consequência da ação da força elástica.
2. O trabalho da força elástica é nulo, pois trata-se de uma força conservativa.
3. O sentido da rotação em torno do centro de forças pode mudar pela ação da força elástica.
4. A energia mecânica sempre aumenta porque sempre há energia potencial armazenada na mola.
5. O momento angular se conserva porque a reta de ação da força elástica sobre a partícula passa pela origem .

Sobre uma mesa horizontal perfeitamente lisa repousa um sistema formado por duas pequenas massas e , ligadas por uma mola de massa desprezível e que se encontra relaxada. A partir do instante passa a atuar sobre a massa uma força externa constante paralela à mesa, e uma força sobre a massa . Pode-se afirmar que para

1. O centro de massa do sistema se move ao longo de uma reta
2. O momento linear total do sistema se conserva
3. A velocidade do centro de massa é uma função quadrática do tempo
4. A distância entre as massas e permanece constante
5. O momento angular total do sistema, referido ao centro de massa, permanece constante

Considere dois discos um de raio e de massa e outro de raio e de massa unidos concentricamente formando um sistema (disco composto) rígido, cujo momento de inércia vale quando gira livremente em torno do eixo fixo e perpendicular ao plano dos discos passando pelo centro. Duas massas, e , presas a cordas finas e inextensíveis enroladas na periferia dos discos de raios e respectivamente, fazem girar o disco composto quando soltas; considere que é o módulo da aceleração local da gravidade.

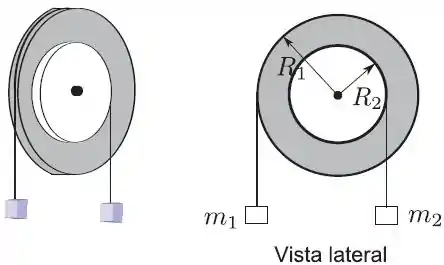
1. Isole os blocos e o disco composto e represente em um diagrama de corpo livre todas as forças, identificando-as, que atuam em cada um deles; use como referência a vista lateral do sistema.
2. Escreva as equações do movimento de rotação do disco composto e de translação dos blocos.
3. Determine a aceleração angular, , do disco composto.
4. Determine matematicamente a condição para que o sistema esteja em equilíbrio

Uma haste homogênea e uniforma, de espessura desprezível, com massa e comprimento , pode girar sem atrito em torno de um pino que passa por uma de suas extremidades, como mostra a figura. O movimento da haste fica restrito a um plano vertical e o módulo da aceleração local da gravidade é igual a .

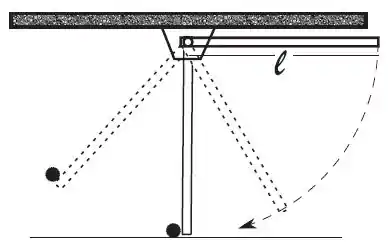
1. Sabendo-se que o momento de inércia da haste em relação a um eixo perpendicular à mesma, e que passe pelo seu centro de massa é igual a , calcule o momento de inércia da haste em relação ao eixo de rotação que passa pelo pino.
2. Se a haste for liberada na posição horizontal, a partir do repouso, determine sua velocidade angular no instante que passa pela posição vertical.

Ainda em relação à situação descrita no ítem anterior, considere que ao passar pela vertical, a exterminadade livre da haste se choque com um pequeno corpo de massa , originalmente em repouso. O corpo de massa adere à haste, e o conjunto continua em movimento de rotação em torno do pino.

3. Calcule o momento de inércia do sistema haste-corpo após a colisão em relação ao pino.
4. Qual é a velocidade angular do sistema haste-corpo de massa , imediatamente após a colisão?