P1 de Física 1 da UFRJ - 2013.2

Um sistema de coordenadas tem origem no solo de uma região plana horizontal, e dessa origem é lançado um projétil que faz um ângulo maior que zero com a horizontal. Ao passar por sua altura máxima o projétil tem uma velocidade e ao atingir o solo tem vetor posição . Podemos afirmar sobre os produtos escalares desses vetores com o vetor aceleração que

1. e
2. e
3. e
4. e
5. e

Uma partícula em trajetória circular de raio tem um vetor aceleração que em um certo instante faz um ângulo com o vetor velocidade . Podemos afirmar que nesse instante

1. O módulo da velocidade da partícula é igual a ;
2. O módulo da velocidade da partícula é igual a ;
3. A aceleração da partícula tem módulo ;
4. O módulo da velocidade da partícula está aumentando;
5. O módulo da velocidade da partícula está diminuindo;

Em um trecho retilíneo de um rio as águas têm velocidade relativa às margens constante e a mesma em todos os pontos do trecho do rio. Um piloto deseja atravessar o rio de modo que a velocidade de seu barco relativa às margens tenha o mesmo módulo que a velocidade das águas relativas às margens, . Além disso, ele deseja seguir uma trajetória retilínea de um ponto da margem até o ponto diretamente em frente a na margem oposta, como indica a figura. Podemos afirmar que o piloto deve imprimir ao barco uma velocidade , relativa às águas de módulo

1. ;
2. ;
3. ;
4. ;
5. ;

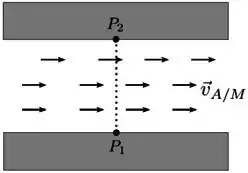
Três macacos , e , de mesmo peso, estão pendurados em repouso, cada um em um cipó, com os cipós amarrados em um galho de árvore. A partir de um dado instante o macaco sobe em seu cipó com velocidade constante, o macaco sobe no seu com aceleração para cima constante e o macaco desce no seu com aceleração para baixo constante. Supondo que os cipós sejam fios ideiais (inextensíveis com massa desprezível), que os movimentos se processem na vertical, que as acelerações mencionadas não sejam nulas, e denotando por , e as tensões nos cipós dos respectivos macacos , e , podemos dizer que

4. e

Um lustre é pendurado em um teto horizontal por dois fios, considerados ideais, que se juntam e são ligados ao lustre, como mostra a figura. Em um dos fios, que faz um ângulo de com o teto, a tensão tem módulo ; no outro, que faz um ângulo com o teto, a tensão tem módulo . Considerando o sistema de eixos com na vertical, como indicado na figura, obtemos que a razão entre as componentes verticais e das tensões é

1. ;
2. ;
3. ;
4. ;
5. ;

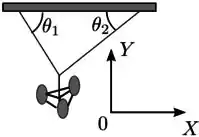
Um bloco abandonado em repouso está descendo com velocidade constante a superfície de um plano inclinado. A força de atrito que a superfície exerce sobre o bloco é

1. Paralela à superfície do plano incilinado com módulo menor que o peso do bloco;
2. Perpendicular à superfície do plano inclinado com módulo menor do que o peso do bloco;
3. Paralela à superfície do plano inclinado com módulo maior do que o peso do bloco;
4. Perpendicular à superfície do plano inclinado com módulo maior do que o peso do bloco;
5. Paralela à superfície do plano inclinado com módulo igual ao peso do bloco.

Um corpo de dimensões desprezíveis e de massa é liberado a partir do repouso da borda de um poço semiesférico de raio . Ele desliza pela parede do poço e após algumas oscilações em torno do fundo do poço permanece em repouso nesta posição. Para as forças presentes desde o inicio até o fim do movimento do corpo é correta a opção

1. O trabalho da força peso é ;
2. O trabalho da força normal que a superfície do poço exerce sobre o corpo não é nulo;
3. O trabalho total das forças dissipativas é nulo;
4. O trabalho total das forças dissipativas é ;
5. O trabalho total das forças dissipativas é ;

Uma partícula se desloca ao longo do eixo , da origem até a posição , onde é uma distância positiva. A única componente da força resultante sobre a partícula, , varia com a posição conforme o gráfico da figura, linearmete da origem a , cortando o eixo em , e também linearmente de até ; no gráfico também está indicado o valor máximo da força. Denotando por , , e as energias cinéticas nas posições , , e , respectivamente, podemos afirmar sobre as variações , e que

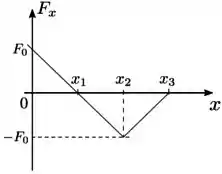
5. e

Os pneus de um carro de massa têm coeficiente de atrito estático com a pista horizontal de uma rodovia em uma curva circular de raio . A velocidade máxima com que o corpo pode fazer essa curva sem derrapar é . Supondo que o carro faça a curva com velocidade de módulo constante , podemos dizer que, nesse caso, a força de atrito estático entre os pneus e a pista tem módulo igual a

Uma partícula move-se no plano em uma trajetória retilínea ao longo do eixo , da origem ao ponto , e a seguir ao longo de uma trajetória retilinea do ponto ao ponto , como inficado na figura. Durante todo o percurso agem sobre a partícula três forças constantes , e de mesmo módulo. Os ângulos que as forças , e fazem com o eixo são, respectivamente, , e . Denotando os respectivos trabalhos das três forças em todo o percurso de a por , e , podemos afirmar que

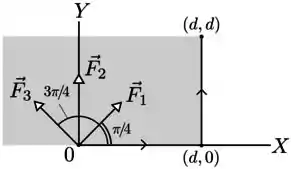
1. , e ;
2. , e ;
3. , e ;
4. , e ;
5. O trabalho realizado por cada uma das três forças é o mesmo.

Uma esfera muito pequena de massa está amarrada a uma haste vertical giratória por dois fios ideiais de comprimento . A haste gira de modo que os fios fiquem tensos formando com a haste um triângulo que mantem seu formato inalterado durante o movimento, conforme ilustra a figura. Sabendo que os fios de cima e de baixo fazem o mesmo ângulo com a horizontal e que a velocidade de rotação da esfera tem módulo constante , determine

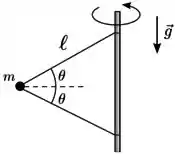
1. O módulo e a orientação (direção e sentido) da força resultante sobre a esfera;
2. O módulo da tensão no fio superior e o módulo da tensão no fio inferior;
3. O limite mínimo do módulo da velocidade de rotação da esfera em torno da haste para que o fio inferior se mantenha esticado.

Um anel de massa , ligado a duas molas de constantes elásticas iguais a e , pode deslizar sem atrito sobre um trilho rígido horizontal, como mostra a figura, na qual está indicado um sistema de eixos , com na direção do trilho. Inicialmente o anel se encontrava em repouso sobre o trilho na posição onde as duas molas estão relaxadas. A partir do instante o anel passou a sofrer a ação de uma força constante , numa direção que faz um ângulo com a horizontal, levando o anel a oscilar em torno de um novo ponto de equilíbrio.

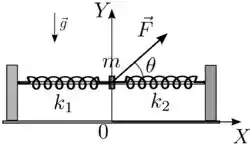
1. Qual a força total que o trilho exerce sobre o anel?
2. Em que posição é nula a resultante das forças que atuam sobre o anel?
3. Escreva a energia potencial elástica do sistema em função da coordenada do anel.
4. Escreva a energia potencial associada à força constante em função da coordenada do anel.
5. Expresse o módulo da velocidade do anel em função de sua coordenada .