P3 de Física 1 da UFRJ - 2022.1

10) Um disco começa a rotacionar com aceleração angular constante em torno de um eixo que passa pelo seu centro. Em certo instante , ele gira a 10 rps (rotações por segundo). Após mais 62,5 voltas, no instante , sua velocidade angular atinge 15 rps. Calcule o intervalo de tempo em segundos.

2. 5,0
3. 31,4
4. 62,8
5. 3,14

11) Uma partícula executa um movimento unidimensional cujo gráfico da componente da velocidade na direção do movimento em função do tempo está ilustrado a seguir.

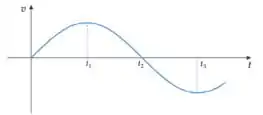
A partir do gráfico, são realizadas as afirmativas

1. No instante , a velocidade da partícula é nula;
2. No instante , a aceleração da partícula é nula;
3. No instante , a componente da velocidade da partícula assume o menor valor considerando o intervalo de tempo ilustrado no gráfico.

São verdadeiras:(a) Somente a II.

(b) Somente a I.(c) Somente a III.

(d) Todas as afirmativas.

(e) Nenhuma das afirmativas.

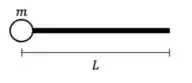
12) Uma barra delgada e uniforme de massa e comprimento tem presa em uma de suas extremidades uma partícula de massa , como mostra a figura. Ao calcularmos o momento de inércia do sistema barra partícula em relação a um eixo passando pelo centro de massa do sistema e perpendicular à barra, encontramos

(a)

(b) (c)

(d) .

(e)

13) Uma bola de massa m cai de uma altura h ricocheteia e sobe até dois terços da altura inicial. Qual é o módulo do impulso exercido pelo piso sobre a bola? Considere o módulo da aceleração da gravidade e despreze a resistência do ar.

(a)

(b) (c)

(d)

(e)

2) A figura a seguir ilustra um dispositivo conhecido como máquina de Atwood, onde dois corpos estão conectados por meio de um fio que passa por uma polia fixa. Considere que as massas dos corpos e valem, respectivamente, e , que a polia pode girar sem atrito em torno do seu eixo e que o fio leve e inextensível não desliza sobre a polia de massa e raio , cujo momento de inércia em relação ao seu eixo de rotação é

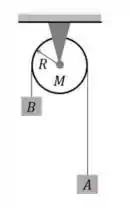
Quando os blocos e são liberados a partir do repouso, em um local onde a aceleração gravitacional

é igual a , a polia adquire uma aceleração angular de módulo igual a:

(a)

(b)

(c)

(d)

(e)

4) Uma esfera homogênea de raio e massa , ao ser abandonada do repouso do alto de uma rampa inclinada em relação à horizontal, desce rolando sem deslizar. Sendo conhecidos os coeficientes de atrito cinético e estático e entre a superfície e a esfera e o módulo Acm da aceleração para a translação do centro de massa da esfera, o módulo da força de atrito que atua sobre a esfera é dado por:

(a) .

(b)

(c)

(d) .

e) .

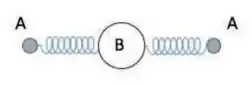
5) Uma molécula tri-atômica linear é formada por dois átomos laterais idênticos A de massa ligados a um átomo central B de massa . Essa molécula apresenta, no caso geral, um movimento de rotação superposto a um movimento de vibração linear em que os dois átomos laterais se aproximam e se afastam simultaneamente do átomo central, como se estivessem presos por duas molas. Se em um dado instante, quando a distância entre os átomos laterais é , o módulo da velocidade angular da molécula é , então o módulo dessa velocidade angular quando a distância mudar para será:

(a)

(b)

(c)

(d)

e)

6) Uma haste delgada e homogênea de comprimento L e massa M que se encontra inicialmente em repouso em uma mesa é atingida ortogonalmente a uma distância d de seu centro por um pequeno disco de massa M/3 que fica a ela aderido após a colisão. Não existindo atrito com a mesa, podemos afirmar que nesse processo de colisão no sistema formado pela haste e o disco não será conservado(a):

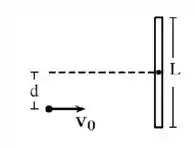
1. Momento linear do sistema.
2. Momento angular do sistema em relação ao centro de massa do sistema.
3. Momento angular do sistema em relação ao centro de da barra.
4. Todas as quantidades mencionadas se conservam.
5. Energia mecânica do sistema.

7) Uma partícula de massa m realiza um loop de raio . No ponto mais alto do loop, o módulo da força normal é . Determine o módulo da velocidade da partícula neste ponto.

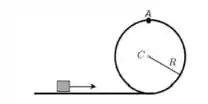
8) Em uma primeira situação, uma barra delgada e homogênea que pode girar em torno de um eixo ortogonal a ela e que passa por uma de suas extremidades tem aplicada na outra extremidade uma forca que é, também, ortogonal a ela. Verifica-se que após um intervalo de tempo de ação da força a barra adquire uma velocidade angular de módulo ao partir do repouso. Na segunda situação, uma outra barra, agora não homogênea em que a massa se encontra concentrada mais próxima ao eixo de rotação, a ação da mesma força e nas mesmas condições acaba produzindo uma velocidade angular final de módulo ao cabo do mesmo intervalo de tempo. Nessas condições, se e forem, respectivamente, os módulos dos momentos angulares finais das duas barras, devemos observar as seguintes relações

1. e
2. e
3. e
4. e
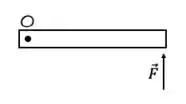
5. e

9) Uma casca esférica homogênea de massa M e raio R é solta do repouso de modo a descer por uma rampa, vindo a abandoná-la a partir de sua extremidade em B, após descer uma altura H, conforme ilustrado na figura. Desconsiderando a resistência do ar e assumindo que a casca nunca perca o contato com a superfície da rampa, a velocidade do centro de massa da casca esférica ao chegar ao ponto B será:

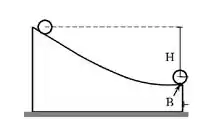
3) Considere uma partícula de massa que é solta do repouso do alto de uma altura de três maneiras distintas. Em nenhum dos casos, há atrito entre o plano e a partícula.

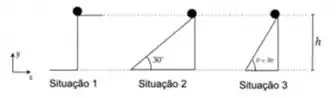
Sejam e os módulos das componentes das velocidades na direção e , e , o trabalho realizado pela força peso após a partícula descer de uma altura nas três situações, é correto afirmar que:

(a) e

(b) e

(c) e

(d) e

(e) e

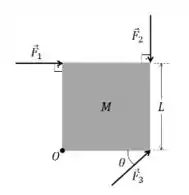
1) Uma placa quadrada de lado tem aplicado em três de seus vértices as forças de mesma intensidade , e cujas orientações são apresentadas na figura, sendo . Ao calcularmos os torques , e produzidos por essas forças em relação ao vértice teremos os seus módulos satisfazendo à seguinte relação:

a)

b)

c)

d)

e)