P2 de Física 1 da UFRJ - 2013.1

Um pescador está sentado no centro de sua canoa que repousa em um lago de águas tranquilas. A sua frente está um cesto com peixes a uma distância . Num dado instante ele muda a posição do cesto colocando-o detrás dele na posição . Considerando o centro de massa do sistema canoa-pescador-cesto e desprezando-se o atrito da água com a canoa, é correta a opção:

1. O centro de massa permanece na posição original;
2. O centro de massa move-se para frente de ;
3. O centro de massa move-se para trás de ;
4. Após mudar o cesto de posição a canoa passa a se movimentar com velocidade uniforme, pois a força resultante sobre o sistema é nula;
5. Nada se pode afirmar pois não são conhecidas as massas da canoa, do pescador e do cesto.

Três partículas de massas , e diferentes movem-se com a mesma velocidade vetorial constante relativas a um dado referencial. Sendo a energia cinética do sistema e a energia cinética do seu centro de massa, relativas a esse referencial inercial, e sua energia cinética relativa ao centro de massa, é correto afirmar que:

1. com e ambas diferentes de zero;
2. com e ambas diferentes de zero;
3. é sempre nula;
4. ;

Um disco homogêneo de massa e raio encontra-se sobre uma mesa horizontal completamente lisa, sem estar preso a ela. Em um dado instante duas forças estão aplicadas tangencialmente na beirada do disco, uma em um ponto diametralmente oposto ao ponto de aplicação da outra. Sabendo que o momento de inércia do disco relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é , e denotado por e os módulos respectivos da aceleração do centro de massa do disco e da aceleração angular de rotação em torno do eixo no instante considerado, podemos dizer que:

1. e ;
2. e ;
3. e ;
4. e ;
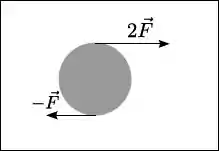
5. e

Um aro elíptico homogêneo de massa é posto para girar com velocidade ao redor do seu eixo maior, em relação ao qual tem momento de inércia . Em seguida, é colocado para girar com mesma velocidade angular ao redor de seu eixo menor, em relação ao qual tem momento de inércia . Veja as figuras. Sobre os módulos dos momentos angulares e dos aros nas respectivas situações e , podemos afirmar que:

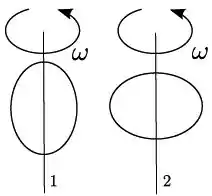
1. , pois o momento de inércia ;
2. , pois trata-se do mesmo sistema girando com a mesma velocidade angular;
3. , pois o momento de inércia ;
4. , pois o momento de inércia ;
5. , pois o momento de inércia ;

Um corpo de massa está suspenso por um fio de massa desprezível enrolado numa polia de raio . A polia consiste em um disco rígido do qual foi retirado um pedaço, como mostra a figura. A polia tem massa e gira sem atrito em torno de um eixo que passa pelo seu centro. Se a massa desce com aceleração de módulo , o momento de inércia da polia é:

1. ;
2. ;
3. ;
4. ;
5. ;

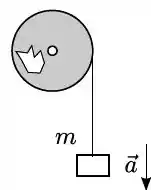
Quatro contas estão presas nos vértices de um arame quadrado de lado , como mostra a figura. Duas contas possuem massa e as outras duas massa . Desprezando a massa do arame e de acordo com o sistema de referência indicado na figura, a posição do centro de massa do arranjo é:

1. e ;
2. e ;
3. e ;
4. e ;
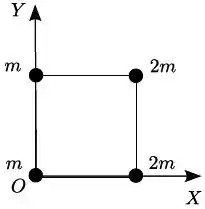
5. e ;

Duas partículas e de massas e movem-se em movimento retilíneo uniforme com velocidades e respectivamente. Num dado instante ocorre uma colisão entre elas totalmente inelástica, pode-se afirmar, sobre a velocidade do centro de massa das partículas que:

1. Depois da colisão ;
2. Antes da colisão ;
3. Depois da colisão ;
4. Antes da colisão e depois da colisão ;
5. Depois da colisão ;

A figura mostra um carrinho de massa , sobre um trilho de ar, que comprime de uma mola de constante elástica . O carrinho está inicialmente preso ao suporte do trilho por um fio. O fio é cortado, e a mola expande-se empurrando o carrinho. Ao passar pela posição de equilíbrio da mola, , o carrinho perde contato com a mola. No trajeto até perder contato com a mola, o impulso fornecido ao carrinho foi igual a:

1. ;
2. ;
3. ;
4. ;
5. ;

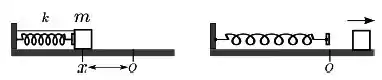
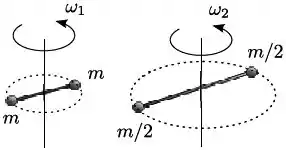
Um haltere é formado por duas partículas de massa , ligadas por uma barra rígida de massa desprezível e comprimento , e gira com velocidade angular em torno de um eixo fixo perpendicular a barra e passando pelo seu ponto médio. Um segundo haltere é formado por duas partículas de massa , ligadas por uma barra rígida de massa desprezível e comprimento , e gira com velocidade angular em torno de um eixo fixo perpendicular a barra e passando pelo seu ponto médio. Considerando que os halteres têm o mesmo momento angular, podemos afirmar que:

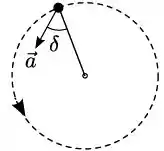
Uma partícula de massa está girando em torno de um eixo (perpendicular a página) com movimento de rotação uniformemente variando com aceleração , como mostra a figura; vista de cima. O raio de trajetória é e o vetor aceleração da partícula tem a sua direção formando um ângulo com a direção radial. Num dado instante ela tem velocidade angular e aceleração angular . Pode-se afirmar que:

1. ;
2. ;
3. ;
4. ;
5. ;

Uma corda de massa desprezível e inextensível está enrolada ao redor de um disco uniforme de raio e de massa e possui a outra extremidade fixada numa barra (conforme mostra a figura). O disco, liberado a partir do repouso, cai com a corda na posição vertical e mantém o seu eixo de rotação sempre na mesma direção. Dado: o momento de inercia de um disco de raio e de massa , segundo um eixo que passa pelo seu centro e perpendicular a sua superfície, é igual a .

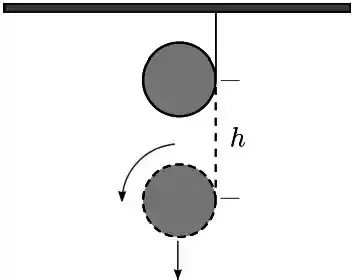
1. Determine a aceleração do centro de massa do disco.
2. Qual é o módulo da tensão na corda?
3. Qual é a velocidade do centro de massa após o disco ter descido uma altura ?
4. Qual é a razão entre as energias cinéticas de rotação e de translação , na mesma situação do item c)?

Dois objetos de mesma massa e dimensões desprezíveis colidem no espaço sideral, na ausência de forças externas. A figura mostra um sistema de eixos de um referencial inercial, com seus unitários e . Antes da colisão os objetos se movem ao longo do eixo com velocidades de sentidos opostos, como indicados na figura, e módulos e , nos quais é uma constante dada. Após a colisão, um os objetos adquire velocidade (na figura de baixo apenas um dos objetos é mostrado).

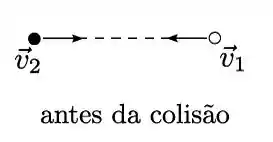
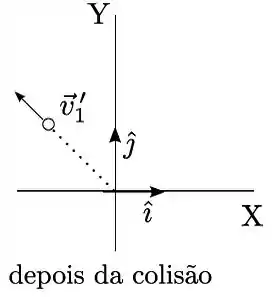
1. Determine a velocidade do outro objeto após a colisão, expressando sua resposta em termos da constante e dos unitários e .
2. Determine a razão entre a energia cinética do par de objetos depois da colisão e sua energia cinética antes da colisão; esta colisão é elástica ou inelástica?