P3 de Física 1 da UFRJ - 2019.2

Um cilindro rígido homogêneo de raio rola sem deslizar para a direita sobre o trecho AB de uma mesa horizontal com velocidade do centro de massa constante de módulo , como mostrado na figura, sendo o coeficiente de atrito estático entre o cilindro e o trecho AB da mesa.

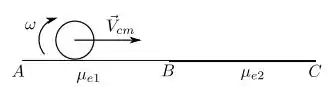
No avanço, entra no trecho BC, no qual o coeficiente de atrito estático com o cilindro é = .

Selecione a resposta correta:

1. O momento angular do cilindro em torno de seu eixo de simetria permanece constante.
2. O cilindro começa a deslizar.
3. A velocidade de translação é duas vezes menor.
4. O torque da força de atrito estática em relação ao eixo de simetria do cilindro é duas vezes maior.
5. A energia cinética total diminui.
6. O cilindro continua rolando sem deslizar, mas a condição de rolamento puro passa a ser .

Um disco horizontal gira com velocidade angular em torno do eixo vertical que passa pelo seu centro. Uma moeda de massa é posta sobre o disco a uma distância do eixo de rotação.

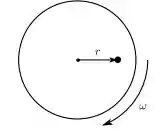
Qual deve ser o coeficiente de atrito mínimo entre a moeda e o disco para que não haja deslizamento?

Um sistema é constituído de quatro massas iguais ligadas por arames rígidos de massas desprezíveis formando um quadrado plano de lado a, no qual as massas estão localizadas nos vértices.

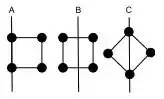
São calculados os momentos de inércia , e relativos aos respectivos eixos A, B e C, mostrados na figura. O eixo A passa lateralmente pelas duas massas, o eixo B pelo centro do quadrado a de dois lados e o eixo C na diagonal. Podemos afirmar, para os momentos de inércia , e, que

Uma correia ideal liga dois discos homogêneos de raios idênticos a e massas e , cuja distância entre os seus centros é . Os seus centros estão fixos por pinos em torno dos quais cada disco pode girar sem atrito. Uma correia tensa e inextensível passa pelas periferias dos discos, sem deslizar sobre elas, e move-se com velocidade de módulo constante , como indica a figura.

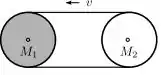
Sabendo-se que o momento de inércia de um disco homogêneo de massa e raio para um eixo que passa pelo seu centro e perpendicular a sua superfície é , podemos afirmar para o módulo do momento angular total do sistema constituído pelos discos, relativo ao seu centro de massa, que

Sob a ação da força de atração gravitacional, um satélite artificial descreve uma órbita elíptica em torno da terra. Qual das quantidades abaixo permanece constante ao longo da trajetória do satélite?

1. O vetor momento angular do satélite em relação ao centro da terra.
2. O módulo do vetor velocidade do satélite.
3. A energia cinética do sistema.
4. O vetor momento linear do satélite.
5. O vetor aceleração tangencial do satélite.

Dois discos homogêneos A e B de massas e raios iguais são fixados por pinos em uma parede vertical, em torno dos quais podem girar sem atrito. Enrola-se em cada um deles um fio ideal em sua periferia, sobre a qual o fio não desliza, e penduram-se blocos de massa iguais a , como mostra a figura.

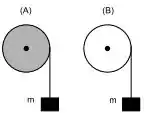
Ao serem os discos A e B libertados a partir do repouso, medem-se, respectivamente, suas acelerações angulares e e os torques sobre eles e , calculados em relação ao centro dos discos. Pode-se relacioná-los corretamente como na opção:

Três cilindros rígidos homogêneos idênticos rolam sem deslizar para a direita sobre uma mesa horizontal. Uma longa placa reta rígida está colocada encima deles e se desloca com velocidade constante módulo como mostrado na figura.

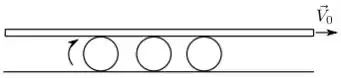
A placa não desliza sobre os cilindros e mantém contato com eles o tempo todo. Podemos afirmar que os cilindros avançam em conjunto com a mesma velocidade de translação de módulo

Uma nave espacial se move em volta da terra com velocidade constante, numa órbita circular de raio . Acionando os foguetes da nave numa determinada sequência, o piloto manobra a nave de maneira a transferi-la para uma nova órbita circular, no mesmo plano, mas de raio . Em relação às variações de energia cinética e potencial gravitacional da nave na transferência entre as duas órbitas, qual afirmação é correta?

1. A energia cinética diminui e a energia potencial aumenta.
2. A energia cinética aumenta e a energia potencial diminui.
3. A energia cinética não se altera e a energia potencial aumenta.
4. A energia cinética não se altera e a energia potencial diminui.
5. As energias cinética e potencial aumentam.

Um anel de espessura desprezível rola sem deslizar sobre uma superfície horizontal. A razão entre as energias cinéticas de rotação e translação do anel é igual a

Uma pequena bola de massa está presa em um fio, apoiada em uma mesa horizontal e sem atrito. A bola executa um movimento circular uniforme com velocidade angular inicial e raio . O fio passa por um furo na mesa. Uma pessoa então puxa o fio lentamente até que o raio da trajetória final torne-se .

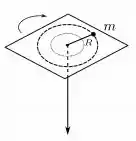
Seja o módulo do momento angular inicial da bola e o módulo do seu momento angular final. Do mesmo modo, é a energia cinética inicial e a energia cinética final. Podemos dizer que

Um bloco de massa desliza para baixo num plano inclinado com velocidade constante desde uma altura acima da base do plano inclinado até a base. O coeficiente de atrito cinético entre o bloco e o plano inclinado é . A energia dissipada pela força de atrito durante essa descida é

Uma barra fina e homogênea de massa e comprimento está pendurada, verticalmente, por sua extremidade superior em um eixo horizontal em torno do qual pode girar sem atrito. Uma bala de massa tem velocidade horizontal de módulo no plano em que a placa pode girar, atinge a barra em repouso a uma distância de sua extremidade superior, e nela fica incrustada, conforme indica a figura.

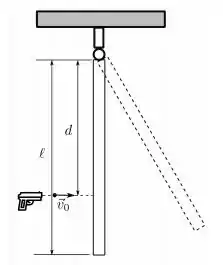
Nessas condições, o conjunto barra+bala adquire velocidade angular de módulo logo após a colisão e então seu centro de massa eleva-se até uma altura máxima . Sabendo que o momento de inércia da barra relativo ao eixo de rotação é , que e , podemos afirmar que