Corpos Rígidos
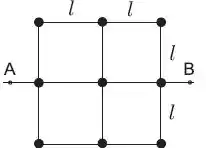
Considere um corpo rígido constituído por: hastes finas, rígidas, de massa desprezível e de comprimento e um conjunto de nove massas iguais a (que podem ser consideradas puntiformes) conforme a figura abaixo. O momento de inércia desse conjunto em torno do eixo é dado por:
Passo 1
O momento de inércia do conjunto é a soma dos momentos de inércia de cada objeto do conjunto.
O momento de inércia de uma partícula em relação ao eixo depende da massa da partícula e da distância da partícula ao eixo. Lembra da fórmula?
Onde é a distância da partícula até o eixo.
Passo 2
Vamos ter partículas no eixo, então seu momento de inércia é zero. Enquanto vamos ter partículas a uma distância do eixo todas com massa então o momento de inércia vai ser
Resposta
Letra C
Exercícios de Livros Relacionados
1. O centro de massa do haltere da FIGURA Q12.1 encontra-se no ponto a, b ou c? Explique.
Uma viga de 40k g e 5,0m de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de 20k g começa a caminhar ao longo da viga. Quão próximo ele pode ch
Integrando diretamente, calcule o momento de inércia de uma haste delgada de Massa M e comprimento L em torno de um eixo localizado a uma distância d de uma das extremidades. Confirme se sua resposta
Uma viga rígida com 3,0m de comprimento e massa de 100k g é apoiada em cada extremidade. Um estudante de 80k g encontra-se em pé a 2,0m do suporte 1. Que valor de força cada suporte exerce sobre a vig
Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu