P1 de Física 1 da USP - 2012

O vetor posição de uma partícula que se move no plano é dado por:

Onde é dado em metros e em segundos. Determine:

(a) o vetor velocidade instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;

(b) o vetor aceleração instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;

(c) o vetor deslocamento da partícula no intervalo de tempo até ;

(d) o vetor velocidade média da partícula no intervalo de tempo até .

Dado:

Um bloco de massa está apoiado sobre o lado esquerdo de um bloco de massa . O coeficiente de atrito cinético entre os dois blocos é de 0,3 e a superfície sobre a qual o bloco de está apoiado é sem atrito. Uma força horizontal constante de módulo é aplicada ao bloco de , colocando-o em movimento como mostrado na figura abaixo. Se a distância que a superfície frontal do bloco menor percorre sobre o bloco maior é de .

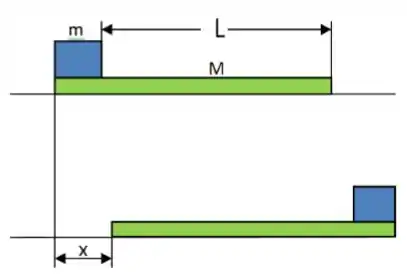
a) Desenhe todas as forças que atuam no sistema

b) Calcule a aceleração do bloco menor em relação ao solo

c) Calcule a aceleração do bloco maior em relação ao solo

d) Qual a distância percorrida pelo bloco maior e quanto tempo o bloco menor levará até chegar ao lado direito do bloco maior?

Você está dirigindo um carro em uma pista circular de raio , que é inclinada de um ângulo com a horizontal, como indicado na Figura. A velocidade do carro é , constante em módulo.

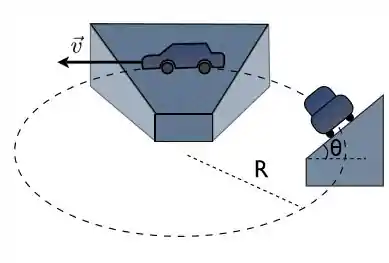
(a) Faça um diagrama de forças considerando que não existe nenhum tipo de atrito entre os pneus do carro e a pista.

(b) Calcule a velocidade na ausência de atrito em função de , e .

(c) Considerando que mesmo com o carro andando há uma força de atrito do tipo estático (de coeficiente ) entre os pneus do carro e a pista, que evita que o carro deslize para baixo ou para cima. Faça o diagrama de forças nestes dois casos.

(d) Com o atrito descrito no item (c) entre o pneu do carro e a pista, determine a velocidade mínima e máxima que o carro pode ter para que este não deslize.

Você tem um estilingue que arremessa projéteis a uma velocidade de , e pretende atingir alguns alvos com esse estilingue. Assuma que .

(a) Qual a distância horizontal máxima que você pode atingir com o seu projétil, assumindo que você atira o projétil desde o solo, e que o alvo também está no solo, na mesma altura do estilingue?

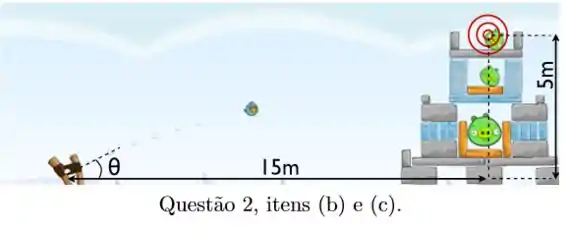
(b) Você quer arremessar o seu projétil (digamos, um “angry bird”) e atingir um alvo (digamos, um porquinho) que se encontra a uma distância de na horizontal, e a uma altura de na vertical, como indicado na Figura. Encontre a equação que determina o valor de a tangente do ângulo com o qual você deverá inclinar o seu estilingue. ( Dica: lembre-se que ).

(c) Agora, considere que entre o seu estilingue e o alvo existe um obstáculo que impede que você lance os projéteis com uma inclinação menor que 60°, ou seja, você só pode lançar projéteis com ângulos . Qual é o valor de que permite que você atinja o seu alvo?