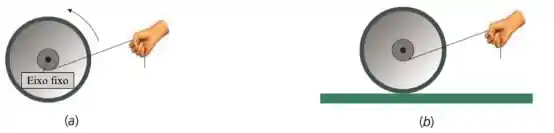Coletâneas de Exercícios de Física 1 da USP - Parte II - Colisões, Torque, Cinemática Angular

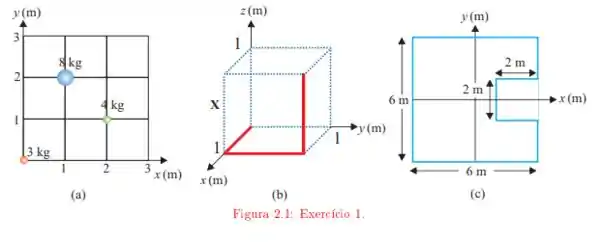
Ache as coordenadas do centro de massa das figuras seguintes. Em considere que os fios tem a mesma densidade linear de massa uniforme. Em considere que a densidade superficial de massa é uniforme.

A posição de três partículas de massas e são dadas (no sistema SI) pelos seguintes vetores posição:

.

a. Determine a posição e a aceleração do centro de massa para um instante t qualquer;

A posição de três partículas de massas e são dadas (no sistema SI) pelos seguintes vetores posição:

.

b. Há forças externas no sistema? Encontre a força externa ou argumente porque não há forças externas.

Um avião explode no ar e se divide em três partes, cujas massas e velocidades imediatamente depois da explosão são (unidades no SI):

.

a. Qual era a velocidade do avião ao explodir?

Um avião explode no ar e se divide em três partes, cujas massas e velocidades imediatamente depois da explosão são (unidades no SI):

.

b. Qual era o seu momento linear?

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

a. Determine a energia cinética dos dois corpos nesse referencial e a velocidade do centro de massa.

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

b. Determine a velocidade de cada um dos corpos em relação ao centro de massa.

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

c. Determine a energia cinética do movimento em relação ao centro de massa.

Um corpo de 5 kg desloca-se para a direita a 5 m/s, perseguindo outro corpo de 3 kg, que se desloca também para a direita a 1 m/s.

d. Determine a energia cinética do movimento do centro de massa.

Um corpo de 3 kg escorrega ao longo de um plano horizontal sem atrito com velocidade . Num certo instante, explode, dividindo-se em duas partes, uma de massa 2 kg e outra de massa 1 kg. Depois da explosão, o pedaço de 1 kg desloca-se com velocidade .

a. Qual a velocidade do pedaço de 2 kg depois da explosão?

Um corpo de 3 kg escorrega ao longo de um plano horizontal sem atrito com velocidade . Num certo instante, explode, dividindo-se em duas partes, uma de massa 2 kg e outra de massa 1 kg. Depois da explosão, o pedaço de 1 kg desloca-se com velocidade .

b. Qual a velocidade do centro de massa depois da explosão?

Um projétil de 6 kg é disparado num ângulo com a horizontal, com velocidade inicial de 40 m/s. No topo da sua trajetória, o projétil explode em dois fragmentos com massas de 2 kg e 4 kg. Os fragmentos deslocam-se na horizontal, imediatamente depois da explosão, e o fragmento de 2 kg cai no lugar do disparo do projétil. Determine:

a. O local onde cai o fragmento de 4 kg;

Um projétil de 6 kg é disparado num ângulo com a horizontal, com velocidade inicial de 40 m/s. No topo da sua trajetória, o projétil explode em dois fragmentos com massas de 2 kg e 4 kg. Os fragmentos deslocam-se na horizontal, imediatamente depois da explosão, e o fragmento de 2 kg cai no lugar do disparo do projétil. Determine:

b. A energia liberada na explosão.

Um homem com 70 kg e um garoto de 35 kg, estão juntos sobre uma superfície gelada, na qual o atrito é desprezível. Um empurra o outro, e o homem se desloca para trás, com velocidade de 0, 3 m/s, em relação ao gelo.

a. Qual a separação dos dois depois de 5 s?

Um homem com 70 kg e um garoto de 35 kg, estão juntos sobre uma superfície gelada, na qual o atrito é desprezível. Um empurra o outro, e o homem se desloca para trás, com velocidade de 0, 3 m/s, em relação ao gelo.

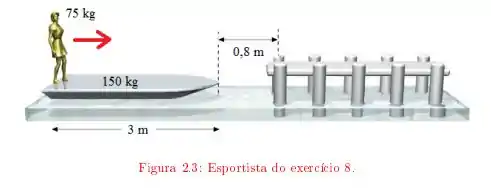
b. A energia mecânica do sistema se conserva?

Uma esportista de 75 kg sentada na popa de uma canoa de 150 kg e 3 m de comprimento, conseguiu encostá-la em uma estaca, onde quer amarrar a canoa. Ao encostar a canoa, ela se levanta e caminha até atingir a outra extremidade, o que leva a canoa a afastar-se da margem. Ela consegue, esticando o braço, alcançar até uma distância de 80 cm da estaca. Conseguirá amarrar a canoa? Caso contrário, quanto falta? Despreze a resistência da água e considere o centro de massa da canoa como localizado em seu ponto médio.

Um garoto de massa 30 kg, correndo a 2, 5 m/s, salta sobre um carrinho de massa 10 kg, que estava parado, permanecendo sobre ele.

a. Determine a velocidade do conjunto carrinho+garoto depois que ambos estiverem andando juntos.

Um garoto de massa 30 kg, correndo a 2, 5 m/s, salta sobre um carrinho de massa 10 kg, que estava parado, permanecendo sobre ele.

b. Em seguida, o garoto começa a andar sobre o carrinho com a velocidade de 0, 5 m/s, relativa ao carrinho, dirigindo-se para frente do mesmo. Qual a nova velocidade do carrinho?

Um garoto de massa 30 kg, correndo a 2, 5 m/s, salta sobre um carrinho de massa 10 kg, que estava parado, permanecendo sobre ele.

c. Quando o garoto chega na extremidade do carrinho, ele pula para frente com velocidade de 1 m/s em relação ao carrinho. Com que velocidade o carrinho fica depois disso?

Um atirador, com um rifle de apoiado ao ombro, dispara uma bala de , cuja velocidade na boca da arma é de .

Com que velocidade inicial a arma recua?

Um atirador, com um rifle de apoiado ao ombro, dispara uma bala de , cuja velocidade na boca da arma é de .

Que impulso transmite ao ombro do atirador?

Um atirador, com um rifle de apoiado ao ombro, dispara uma bala de , cuja velocidade na boca da arma é de .

Se o impulso é absorvido pelo ombro em , qual é a força média exercida sobre ele?

Uma bala de 10 g é disparada sobre um pêndulo balístico de massa 990 g.

a. Se a velocidade inicial da bala é 300 m/s, qual a altura atingida pelo pêndulo (junto com a bala) depois da colisão?

Uma bala de 10 g é disparada sobre um pêndulo balístico de massa 990 g.

b. Se a velocidade inicial da bala é 200 m/s, determine a altura máxima atingida pelo pêndulo quando a bala passa através dele e emerge com velocidade de 50 m/s.

Um bloco de madeira, de 1, 0 kg, está ligado a uma mola de constante de força 200 N/m e repousa sobre uma superfície horizontal lisa. Uma bala de 20 g atinge o bloco e comprime a mola de 13, 3 cm.

a. Calcular a velocidade da bala antes da colisão.

Um bloco de madeira, de 1, 0 kg, está ligado a uma mola de constante de força 200 N/m e repousa sobre uma superfície horizontal lisa. Uma bala de 20 g atinge o bloco e comprime a mola de 13, 3 cm.

b. Que fração da energia mecânica inicial se perde na colisão?

Um vagão de 20 toneladas está freado no topo de uma descida. Em dado instante ele é solto, rola pela ladeira, descendo 9 m em relação à posição original. Na parte mais baixa da ladeira, ele engata em outro vagão, de 10 toneladas, que está livre nos trilhos. Os dois, engatados, sobem uma ladeira até uma altura H. Calcular H.

Um corpo de 4 kg, deslocando-se a 5 m/s, efetua uma colisão perfeitamente elástica com um corpo de 1 kg, inicialmente em repouso. Determine a velocidade final de cada corpo e a energia transferida para o corpo de 1 kg.

Uma bala de massa igual a 4, 5 g é disparada horizontalmente num bloco de madeira de massa igual a 2, 4 kg, em repouso sobre a superfície horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale 0,20. A bala fica retida no bloco que sofre um deslocamento de 1, 8 m até o repouso.

a. Qual a velocidade do bloco imediatamente após a bala parar em seu interior?

Uma bala de massa igual a 4, 5 g é disparada horizontalmente num bloco de madeira de massa igual a 2, 4 kg, em repouso sobre a superfície horizontal. O coeficiente de atrito cinético entre o bloco e a superfície vale 0,20. A bala fica retida no bloco que sofre um deslocamento de 1, 8 m até o repouso.

b. Qual a velocidade inicial da bala?

Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.

a. Qual o trabalho realizado pelas forças que atuam sobre a bola?

Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.

b. Quais as velocidades dos corpos após a colisão?

Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.

c. Até que altura sobe a bola após a colisão?

Uma bola de massa m = 0, 5 kg é presa a um pino por um o leve e inextensível de 0, 8 m de comprimento. A bola é abandonada quando está na horizontal. Na parte mais baixa da trajetória a bola atinge um bloco de massa M = 2, 0 kg, inicialmente em repouso sobre uma superfície áspera. A colisão, entre a bola e o bloco, pode ser considerada como perfeitamente elástica. O coeficiente de atrito cinético entre o bloco e a superfície é µc = 0, 16.

d. Qual a distância percorrida pelo bloco depois da colisão?

Um caminhão carregado, M = 3 ton, viajando para o norte a 60 km/h, colide com um carro de massa total m = 1 ton, trafegando para leste a 90 km/h, num cruzamento. Calcule em que direção e de que distância o carro é arrastado pelo caminhão, sabendo que o coeficiente de atrito cinético no local do acidente é 0,5.

Uma bola deslocando-se a 10 m/s, faz uma colisão perfeitamente elástica, mas oblíqua, com uma outra bola de mesma massa e em repouso. A bola incidente é desviada de 30◦ em relação à direção inicial do movimento. Determinar a velocidade de cada bola depois da colisão.

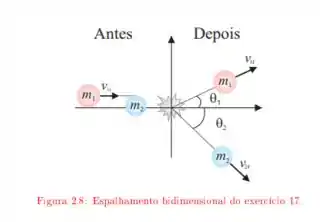
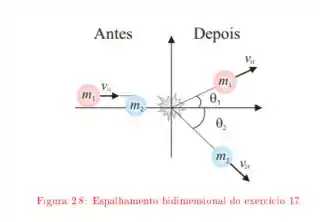
Num choque entre dois corpos de massas e , o primeiro desvia 90◦ de sua trajetória original, mantendo inalterada sua energia cinética. Se as velocidades iniciais dos corpos eram, respectivamente, e :

a. Calcule o vetor velocidade de após a colisão.

Num choque entre dois corpos de massas e , o primeiro desvia 90◦ de sua trajetória original, mantendo inalterada sua energia cinética. Se as velocidades iniciais dos corpos eram, respectivamente, e :

b. Verifique se o choque foi elástico ou inelástico.

Os corpos estão ligados por barras muito leves cujos momentos de inércia podem ser desprezados. O sistema gira em torno do eixo y com velocidade angular.

a. Considere que no instante t = 0 s, os corpos estejam nas posições indicadas na figura. Determine o vetor velocidade de cada partícula usando o produto vetorial ⃗v = ⃗ω × ⃗r.

Os corpos estão ligados por barras muito leves cujos momentos de inércia podem ser desprezados. O sistema gira em torno do eixo y com velocidade angular.

b. Use a velocidade escalar de cada corpo para calcular a energia cinética do sistema.

Os corpos estão ligados por barras muito leves cujos momentos de inércia podem ser desprezados. O sistema gira em torno do eixo y com velocidade angular.

c. Determine o momento de inércia do sistema em torno do eixo y e calcule a energia cinética do sistema utilizando a relação .

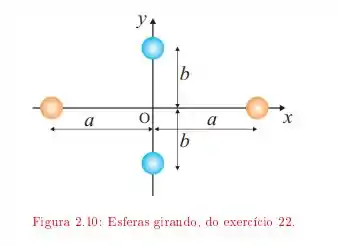
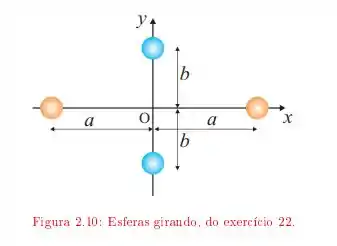
Quatro esferas pequenas de massa m estão presas às extremidades de uma estrutura de massa desprezível no plano xy.

a. Se a rotação do sistema ocorre ao redor do eixo y com velocidade angular ω, encontre o momento de inércia Iy ao redor do eixo y e a energia cinética rotacional ao redor desse eixo.

Quatro esferas pequenas de massa m estão presas às extremidades de uma estrutura de massa desprezível no plano xy.

b. Supondo que o sistema gire no plano xy ao redor de um eixo passando por O (eixo z), calcule o momento de inércia ao redor do eixo z e a energia rotacional ao redor desse eixo.

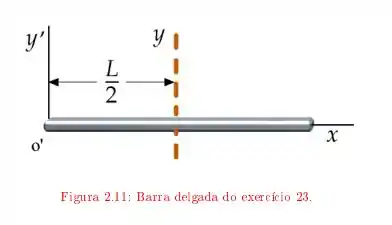
Uma barra na, com uma distribuição de massa uniforme, tem massa M e comprimento L. Calcule o seu momento de inércia em relação a um eixo (y) que passa pelo centro da barra e é perpendicular ao plano xz . Usando o teorema dos eixos paralelos, determine o momento de inércia em relação ao eixo y ′ , que passa por O′ e é paralelo ao eixo y.

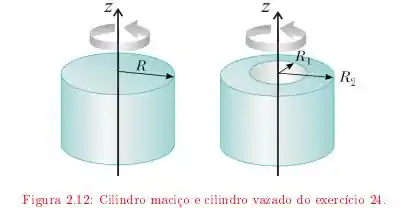
Um cilindro maciço de raio e massa tem . Utilizando este resultado, calcule o momento de inércia de um cilindro uniforme vazado de massa , de raio interno e externo , em relação ao eixo [veja a figura ].

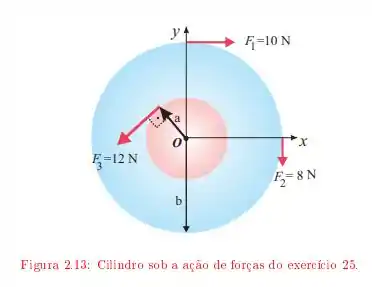
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .

Qual é o torque exercido sobre o cilindro?

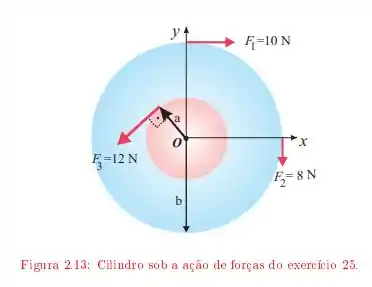
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .

Qual é o vetor aceleração angular do cilindro?

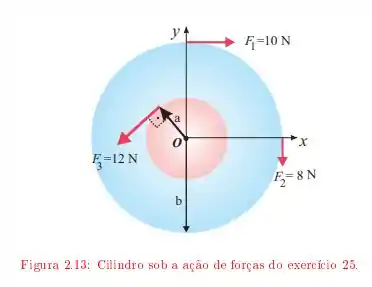
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .

Sabendo que a velocidade angular inicial do cilindro era , determine .

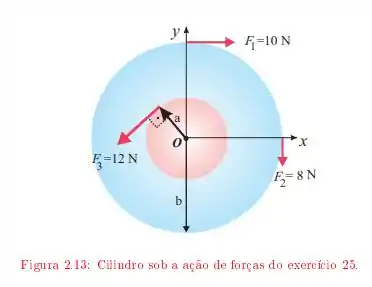
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .

Qual é a sua energia cinética depois de ?

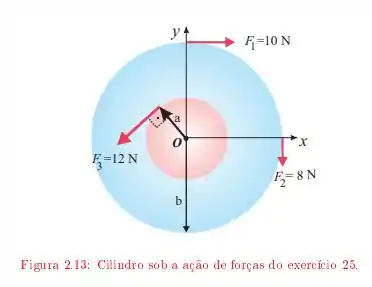
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .

Determine o ângulo total que o cilindro gira em . Verifique que o trabalho efetuado pelo torque é igual a energia cinética.

Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .

Determine a aceleração, a velocidade e a posição do centro de massa em função do tempo.

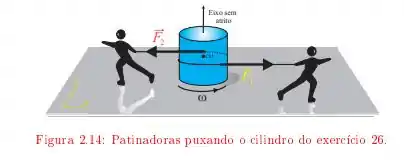
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .

Quais são a aceleração angular e a velocidade angular em função do tempo?

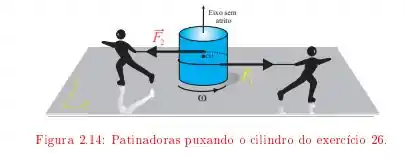
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .

Quantas voltas em torno de seu eixo o cilindro faz durante este tempo?

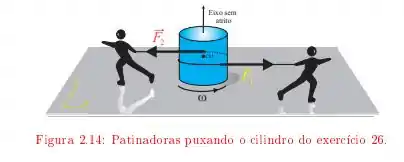
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .

calcule a energia cinética do cilindro quando .

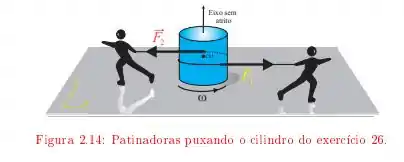
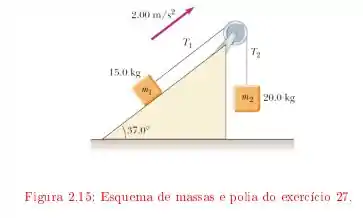
Dois blocos estão ligados por um fio de massa desprezível passando sobre uma polia de raio e momento de inércia . O bloco sobre o plano inclinado sem atrito está subindo com uma aceleração constante de .

Determine e , as duas tensões nas duas partes do fio.

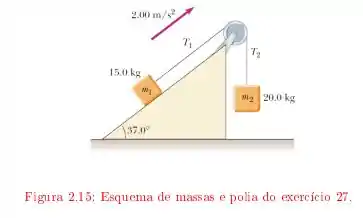
Dois blocos estão ligados por um fio de massa desprezível passando sobre uma polia de raio e momento de inércia . O bloco sobre o plano inclinado sem atrito está subindo com uma aceleração constante de .

Encontre o momento de inércia da polia.

Uma partícula de massa move-se com velocidade constante em uma trajetória retilínea, como mostra figura .

Qual é o momento angular dessa partícula em relação ao ponto ? E em relação ao ponto ?

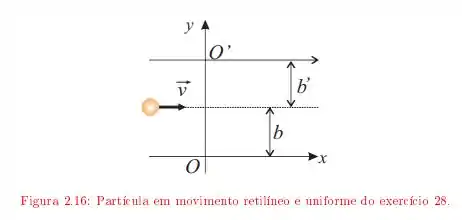
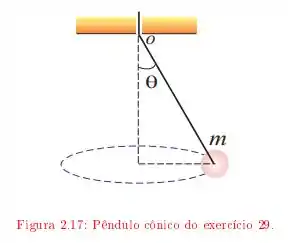
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a . O fio passa sem atrito através de um orifício numa placa, e é puxado lentamente para cima até que o ângulo passa a .

Que comprimento do fio foi puxado?

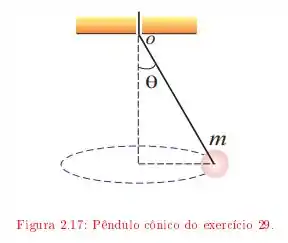
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a . O fio passa sem atrito através de um orifício numa placa, e é puxado lentamente para cima até que o ângulo passa a .

Qual foi a variação da velocidade de rotação?

Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .

Calcule o vetor momento angular do sistema e mostre que é o mesmo em relação a qualquer ponto e se conserva.

Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .

Quando os dois patinadores chegam a uma distância um do outro, estendem os braços e dão-se as mãos, passando a girar em torno do centro de massa do sistema. Calcule a velocidade angular.

Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .

Calcule a energia cinética do sistema antes e depois dos patinadores se unirem. Explique o resultado.

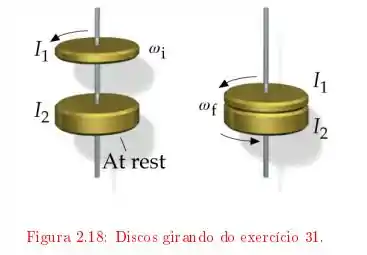
Um disco com momento de inércia , está girando, com velocidade angular em torno de um eixo sem atrito. Num certo instante, este disco cai sobre outro disco, de momento de inércia , que está inicialmente em repouso, no mesmo eixo. Em virtude do atrito entre as superfícies, os dois discos terminam por atingir uma velocidade angular comum a ambos . Determine . A energia cinética do sistema se conserva?

Uma porta de e de largura, suspensa por dobradiças bem azeitadas, está aberta de , ou seja, com seu plano perpendicular ao plano do batente. Ela leva um empurrão na beirada aberta, com impacto equivalente ao de uma massa de com velocidade de . Quanto tempo ela leva para fechar-se?

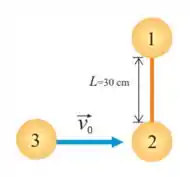
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.

(a) Determine o vetor posição do centro de massa em função do tempo.

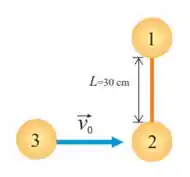
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.

(b) Determine o vetor velocidade do centro de massa.

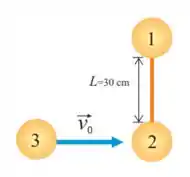
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.

(c) Determine a velocidade angular do sistema depois da colisão.

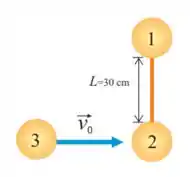
33. Um haltere formado por dois discos e iguais de massa unidos por uma barra rígida de massa desprezível e comprimento repousa sobre uma mesa de ar horizontal. Um terceiro disco de mesma massa , desloca-se com atrito desprezível e velocidade sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco , ficando colado a ele.

(d) Determine a fração da energia mecânica inicial que é perdida no impacto.

34. Uma mesa de coquetel tem um tampo giratório, que é uma tábua circular de raio e massa , capaz de girar com atrito desprezível em torno de um eixo vertical da mesa. Uma bala de massa e velocidade , disparada por um convidado, numa direção horizontal, vai encravar-se na periferia da tábua.

(a) Qual é a velocidade angular de rotação adquirida pela tábua?

34. Uma mesa de coquetel tem um tampo giratório, que é uma tábua circular de raio e massa , capaz de girar com atrito desprezível em torno de um eixo vertical da mesa. Uma bala de massa e velocidade , disparada por um convidado, numa direção horizontal, vai encravar-se na periferia da tábua.

(b) Que fração da energia cinética inicial é perdida no impacto?

35. Um alçapão quadrado de lado e massa está levantado verticalmente, em equilíbrio sobre as dobradiças, quando é levado a cair por uma ligeira trepidação. Desprezando o atrito, que velocidade angular terá adquirido ao bater no chão?

36. Um bloco de massa , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio e massa , a uma massa suspensa . O sistema é solto em repouso. Calcule, por conservação da energia, a velocidade de após cair de uma altura .

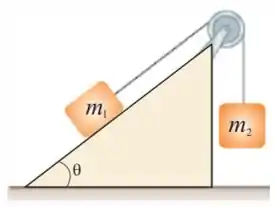
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.

(a) Qual é a tensão no fio?

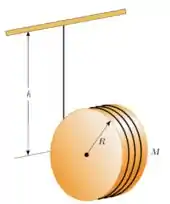
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.

(b) Qual é o módulo da aceleração do centro de massa?

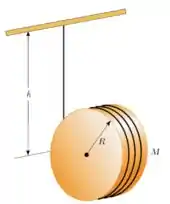
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.

(c) Qual é a velocidade do centro de massa depois que o disco desce uma distância vertical ?

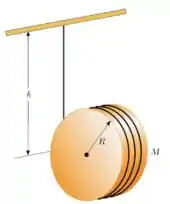
37. Um cilindro uniforme de raio e massa tem um fio enrolado sobre a sua superfície. O disco é solto do repouso com o fio vertical e com sua extremidade superior presa a uma barra fixa.

(d) Verifique a resposta anterior utilizando o enfoque da energia.

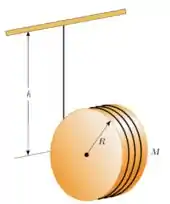
38. Uma roda cilíndrica de raio e massa , rola sem deslizar sobre um plano horizontal, deslocando-se com velocidade , e sobe sobre um plano inclinado de inclinação , continuando a rolar sem deslizamento. Até que altura o centro da roda subirá sobre o plano inclinado?

39. Uma bola de boliche esférica de massa e raio é lançada com velocidade horizontal e não tem qualquer rotação. O coeficiente de atrito cinético entre a bola e a pista é .

(a) Achar o tempo que a bola escorrega até atingir a condição de rolamento sem deslizamento.

39. Uma bola de boliche esférica de massa e raio é lançada com velocidade horizontal e não tem qualquer rotação. O coeficiente de atrito cinético entre a bola e a pista é .

(b) A distância que a bola percorre antes de principiar a rolar sem escorregar.

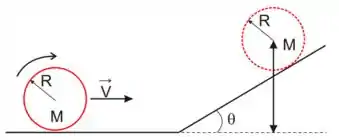
40. Uma bola de futebol, de massa e com diâmetro , rola sem deslizar sobre um plano inclinado. Ela parte do repouso e, depois de e tendo completado exatamente rotações, escapa pela borda do plano inclinado. Dado: .

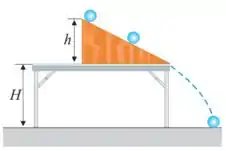
(a) Calcule o torque resultante sobre a bola relativo ao seu centro de massa, enquanto ela rola sobre o plano inclinado.

40. Uma bola de futebol, de massa e com diâmetro , rola sem deslizar sobre um plano inclinado. Ela parte do repouso e, depois de e tendo completado exatamente rotações, escapa pela borda do plano inclinado. Dado: .

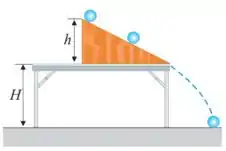
(b) Calcule a energia de rotação da bola ao colidir com o solo

41. Uma bola homogênea de raio rola sem deslizar, a partir do repouso, desde o topo de um domo hemisférico de raio .

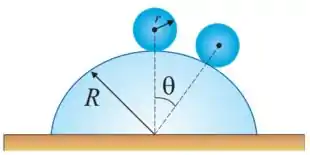
(a) Depois de percorrer que ângulo em relação à vertical a bola deixará a superfície?

41. Uma bola homogênea de raio rola sem deslizar, a partir do repouso, desde o topo de um domo hemisférico de raio .

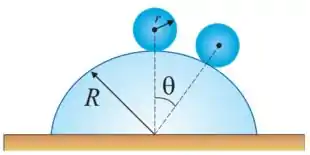
(b) Com que velocidade isso acontece?

42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .

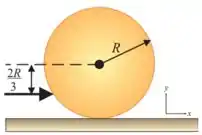
(a) Qual a velocidade angular inicial ?

42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .

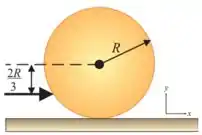
(b) Qual a velocidade da bola uma vez iniciado o rolamento sem escorregamento?

42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .

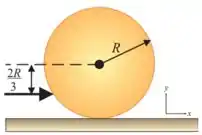
(c) Qual a energia cinética inicial da bola? Assuma e .

42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .

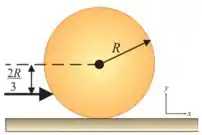
(d) Qual o trabalho da força de atrito?

43. Para um disco de massa e raio , que rola sem delizar, o que é maior, sua energia cinética translacional ou sua energia cinética de rotação em relação ao centro de massa?

(a) A energia cinética de rotação em relação ao centro de massa é maior.

(b) A resposta depende da massa do disco.

(c) As duas energias são iguais

(d) A resposta depende do raio do disco.

(e) A energia cinética translacional é maior.

44. Um sistema formado por dois baldes e uma barra estão fixados a um eixo como indicado na figura. O sistema, que gira em torno do eixo com uma certa velocidade angular, descreve um círculo no plano perpendicular ao eixo. De repente começa a chover. Despreze qualquer tipo de atrito e força de resistência. Pode-se afirmar que:

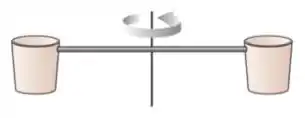
(a) Os baldes continuam girando com a mesma velocidade angular constante como consequência da conservação do momento angular do sistema baldes+barra+chuva.

(b) Os baldes giram com maior velocidade angular porque o momento angular do sistema baldes+barra é conservado.

(c) Os baldes giram com menor velocidade angular como consequência da conservação do momento angular e da energia mecânica do sistema baldes+barra+chuva.

(d) Os baldes giram com menor velocidade angular porque o momento angular do sistema baldes+barra+chuva é conservado.

45. Um objeto quadrado de massa é formado por quatro varetas finas idênticas, todas de comprimento e massa , amarradas juntas. O objeto é fixado a uma barra, podendo girar em torno dela com velocidade angular , como mostrado na figura. O momento de inércia do objeto, em relação ao eixo de rotação (eixo z) na figura é:

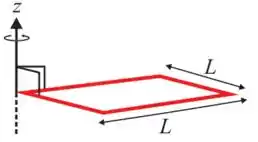
(a) .

(b) .

(c) .

(d) .

(e) .

46. Duas barras idênticas, de mesma massa e comprimento, são usadas para desenhar um objeto com a forma da letra . Cada objeto pode girar em torno do eixo indicado pela linha tracejada na figura. Para os momentos de inércia a , relacionados com a rotação em torno ao eixo indicado, pode-se afirmar que:

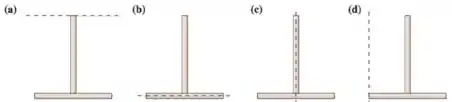
(a) .

(b) .

(c) .

(d) .

(e) .

47. Durante uma exibição, um patinador está girando em torno de um eixo vertical com os braços estendidos horizontalmente. Em um certo instante, quando ele aproxima os dois braços do estômago, pode-se afirmar que:

(a) O seu momento de inércia diminui, o seu momento angular permanece constante e sua energia mecânica aumenta.

(b) O seu momento de inércia, momento angular e energia cinética diminuem.

(c) O seu momento angular permanece constante e sua energia cinética diminui.

(d) O seu momento de inércia aumenta, e seu momento angular e energia mecânica permanecem constantes.

(e) O seu momento de inércia, momento angular e energia cinética aumentam.

Um carretel é livre para girar em torno de um eixo fixo, e um cordão enrolado em torno do seu eixo faz com que ele gire no sentido anti-horário como indicado na . No entanto, se o carretel é colocado sobre uma mesa horizontal , com o ângulo entre o fio e a horizontal igual ao da , e se há força de atrito suficiente entre ele e a mesa, podemos dizer que tal carretel:

Considere o espalhamento elástico entre uma partícula alfa de massa por um nêutron em repouso, de massa como mostra a figura.

a. Qual é o ângulo máximo de espalhamento ? Neste ângulo, que fração da energia cinética incidente vai para o nêutron?

Considere o espalhamento elástico entre uma partícula alfa de massa por um nêutron em repouso, de massa como mostra a figura.

b. Qual é o ângulo entre a direção de recuo e a de incidência?