P3 de Física 1 da USP - 2018

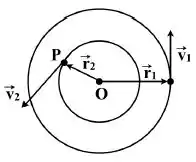
Um ponto material , com massa , esta amarrado com uma corda inextensível a uma haste vertical fina, posicionada no ponto O. A haste gira e produz uma trajetória circular do ponto , com raio inicial , velocidade inicial e velocidade angular . Após algum tempo, a corda foi envolta em torno da haste e o raio da própria trajetória é reduzido para um valor final . Podemos afirmar, em relacao às magnitudes da velocidade final () e da velocidade angular final () de , que:

(a) e

(b) a) e c) sao corretas

(c) Nenhuma é correta

(d) ,

(e) e

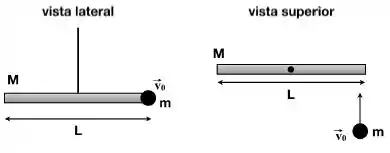
Uma haste, muito fina e homogênea, de massa e comprimento está inicialmente parada, suspensa por um fio que passa pela metade da barra (considere o fio inextensivel e de massa despreziavel). Um projétil de massa é lançado, com velocidade perpendicular à barra contra um dos seus extremos, de forma que o projétil permanece cravado na barra e o sistema começa a girar num plano perpendicular ao eixo do fio. Nestas condições, o módulo da velocidade angular () será dado por:

Dados: (barra)

(a)

(b)

(c)

(d)

(e)

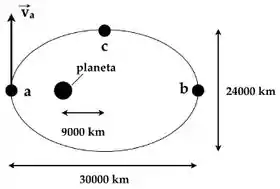
Um satélite segue a órbita elíptica da figura abaixo. A única força sobre o satélite é a atração gravitacional do planeta. A massa do satélite pode ser tomada como sendo completamente desprezível comparada àquela do planeta. A magnitude da velocidade do satélite no ponto a é . A magnitude da velocidade do satélite no ponto b é:

(a) impossível de determinar sem que as massas do planeta e do satélite sejam fornecidas.

(b) , já que o trabalho realizado pela força gravitacional sobre o satélite é nulo.

(c) , por conservação de momento linear do sistema satélite-planeta.

(d) , devido à conservação de momento angular do satélite.

(e) maior que , já que a velocidade angular do satélite é constante e .

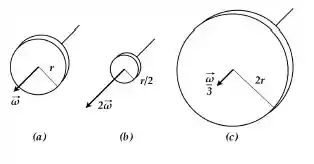
A figura mostra três discos homogêneos e feitos do mesmo material em rotação em torno de seus eixos de simetria. O ordenamento correto das energias rotacionais dos discos é:

Dados: (cilindro)

(a)

(b)

(c)

(d)

(e)

No espaço sideral, longe da influência gravitacional de qualquer planeta ou estrela, dois veículos espaciais munidos de fogutes estão acoplados a uma estação espacial longa de de comprimento. O sistema todo encontra-se em repouso. A massa de um dos veículos é e a do outro . A massa da estação espacial é e esta pode ser considerada como um cilindro delgado homogêneo. Os foguetes são acionados simultaneamente, de forma que a magnitude da força de reação dos gases de exaustão sobre cada veículos (i.e., o empuxo) é de e pode ser considerada perpendicular à estação espacial.

Importante: Quando necessário, faça substituições numéricas apenas nas expressões analíticas finais. Quantidades vetoriais devem ser expressas num sistema de coordenadas com uma base apropriada de versores.

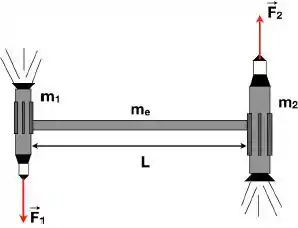
Dados: (barra)

(a) Calcule a posição do centro de massa CM do sistema “veículos + estação espacial” com respeito à posição do centro de massa da estação espacial. Trate os veículos como massas pontuais.

(b) Escreva a equação de movimento para o CM do sistema do ítem (a) num referencial inercial antes e depois do acionamento dos foguetes. Que movimento descreve o CM após o acionamento?

(c) Determine o momento de inércia do sistema do ítem (a) com respeito a um eixo passando pelo seu CM e perpendicular ao plano de movimento dos veículos após o acionamento dos foguetes.

(d) Determine o vetor torque total com respeito ao CM devido ao empuxo dos foguetes.

(e) Calcule a magnitude da velocidade angular de rotação do sistema após o acionamento dos motores.