Coletâneas de Exercícios de Física 1 da USP - Parte I - Cinemática, Leis de Newton, Trabalho e Energia
Física 1 - USP
A posição de uma pedra que cai do alto de um rochedo, a partir do repouso, é dada por , medida para baixo a partir da posição inicial .
a. Se é o deslocamento da pedra e a velocidade média, o que você conclui analisando os dados da tabela seguinte?
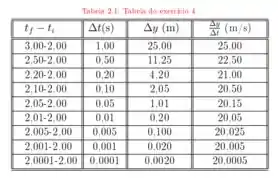
A posição de uma pedra que cai do alto de um rochedo, a partir do repouso, é dada por , medida para baixo a partir da posição inicial .
b. Calcule e avalie esta derivada em .
Ver solução completaUm carro A, inicialmente em repouso, parte do início de uma pista de de comprimento com aceleração . No mesmo instante, um carro B, também em repouso, parte do final da mesma pista, no sentido contrário, com aceleração .
a. Em uma mesma escala faça os gráficos da velocidade dos carros A e B em função do tempo e calcule suas acelerações no instante ;
Ver solução completaUm carro A, inicialmente em repouso, parte do início de uma pista de de comprimento com aceleração . No mesmo instante, um carro B, também em repouso, parte do final da mesma pista, no sentido contrário, com aceleração .
b. Em uma mesma escala, faça os gráficos das posições e dos carros para o intervalo de tempo e determine a distância percorrida pelo carro A do início do movimento até o instante em que ele cruza com o carro B.
Ver solução completaUm objeto é lançado verticalmente, em com uma velocidade de para cima, de uma janela situada a do solo.
Determina a expressão considerando o eixo de referência orientado para cima;
Ver solução completaUm objeto é lançado verticalmente, em com uma velocidade de para cima, de uma janela situada a do solo.
b) Faça o gráfico de
Ver solução completaUm objeto é lançado verticalmente, em com uma velocidade de para cima, de uma janela situada a do solo.
c) Calcule o deslocamento do objeto para os intervalos e ;
Ver solução completaUm objeto é lançado verticalmente, em com uma velocidade de para cima, de uma janela situada a do solo.
d) Determine a distância total percorrida para o intervalo e a altura máxima que o objeto atinge.
Ver solução completaUma bola é arremessada verticalmente para cima, partindo do chão, com uma velocidade de .
Quanto tempo levará para atingir o ponto mais alto da trajetória?
Ver solução completaUma bola é arremessada verticalmente para cima, partindo do chão, com uma velocidade de .
Que altura a bola atingirá.
Ver solução completaUma bola é arremessada verticalmente para cima, partindo do chão, com uma velocidade de .
c) Em que instante a bola estará a do chão?
Ver solução completaUma bola é arremessada verticalmente para cima, partindo do chão, com uma velocidade de .
d) Quanto tempo levará até a bola retornar ao chão?
Ver solução completaUma bola é arremessada verticalmente para cima, partindo do chão, com uma velocidade de .
e) Qual a distância total percorrida pela bola?
Ver solução completaUm objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
Qual é o sentido dessa aceleração em relação ao eixo de referência?
Ver solução completaUm objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
Qual a expressão da velocidade no intervalo ?
Ver solução completaUm objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
c) Calcule sua aceleração média durante esses .
Ver solução completaUm objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
d) Determine a expressão da posição sabendo que em o corpo está passando pela posição .
Ver solução completaUm objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
e) Calcule o deslocamento do corpo nos primeiros segundos do movimento;
Ver solução completaUm objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
f) Calcule a velocidade média do objeto durante os segundos.
Ver solução completaUm objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
a) Faça o gráfico da velocidade em função do tempo para o intervalo de tempo , indicando os instantes em que a velocidade é nula e em que ela é máxima (positiva);
Ver solução completaUm objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
b) O deslocamento do corpo no intervalo
Ver solução completaUm objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
c) O tempo que ele leva para voltar à mesma posição, sabendo que partiu, em , da posição ;
Ver solução completaUm objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
d) A distância total percorrida nos do movimento.
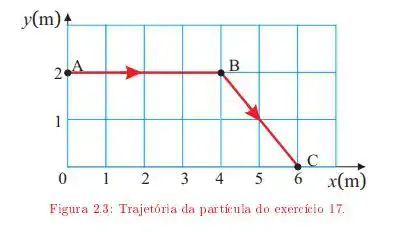
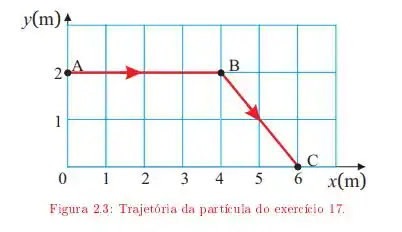
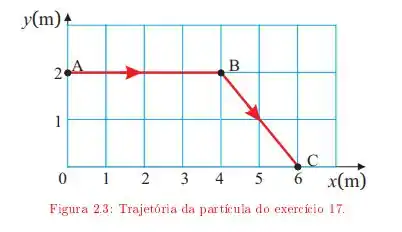
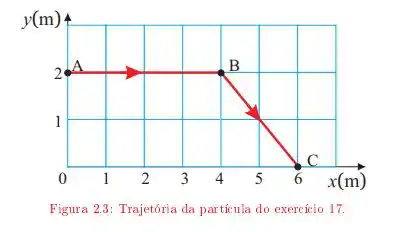
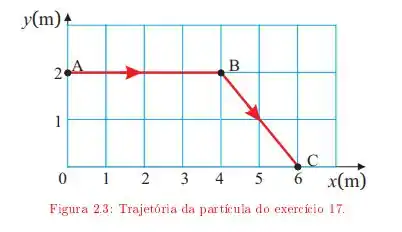
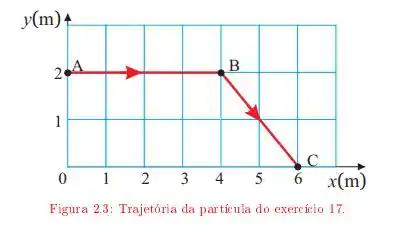
Ver solução completaUma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
a. O vetor velocidade em função do tempo, no trecho AB da trajetória;
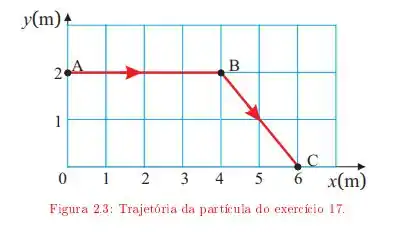
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
b. O vetor posição em função do tempo, no trecho AB da trajetória;
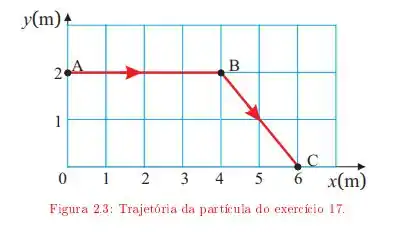
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
c. O tempo que a partícula leva para sair de A e chegar em B;
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
d. O vetor velocidade em função do tempo, no trecho BC da trajetória;
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
e. O vetor posição em função do tempo, no trecho BC da trajetória;
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
f. O tempo que a partícula leva para sair de A e chegar em C;
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
g. O módulo do vetor deslocamento entre A e C;
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:
h. A distância total percorrida pela partícula entre os instantes t = 0 e t = 3 s.
Dois objetos A e B iniciam seus movimentos, simultaneamente, nas posições e . Decorridos 5 segundos o corpo A chega em enquanto o corpo B chega em .
a. Qual dos dois corpos teve o maior deslocamento? Calcule e desenhe esses vetores;
Ver solução completaDois objetos A e B iniciam seus movimentos, simultaneamente, nas posições e . Decorridos segundos o corpo A chega em enquanto o corpo B chega em .
b. Supondo que os deslocamentos foram retilíneos e uniformes, calcule a distância entre os dois corpos, em função do tempo, para o intervalo e a distância entre eles para .
Ver solução completaUm objeto tem aceleração constante . No instante , a velocidade é zero e o vetor posição é .
a. Determine o vetor velocidade e o vetor posição em função do tempo;
Ver solução completaUm objeto tem aceleração constante . No instante , a velocidade é zero e o vetor posição é .
b. Determine a equação da trajetória no plano xy e faça um desenho desta.
Ver solução completaUma partícula A move-se ao longo da reta , com uma velocidade constante (m/s). Uma segunda partícula, B, começa a movimentar-se, a partir da origem, com velocidade inicial nula e com aceleração constante , tal que , no mesmo instante em que a partícula A passa pelo eixo y. Qual deve ser o valor do ângulo θ, entre o vetor e o eixo y, para que, nesta situação, ocorra uma colisão entre A e B? Em que posição a colisão ocorreu?
Ver solução completaA posição de uma partícula em função do tempo é dado por:
onde está em metros e em segundos.
(a) Calcule o vetor aceleração e mostre que a sua direção é radial e que seu módulo é ;
Ver solução completaA posição de uma partícula em função do tempo é dado por:
onde está em metros e em segundos.
(b) Qual o período do movimento?
Ver solução completaUma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:
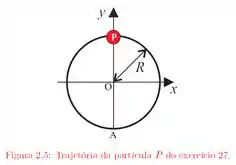
(a) O módulo e a direção dos vetores que descrevem sua posição , e segundos mais tarde;
Ver solução completaUma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:
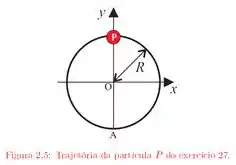
(b) O módulo e a direção do vetor deslocamento no intervalo de tempo de segundos a contar do quinto segundo;
Ver solução completaUma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:
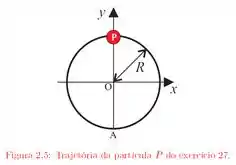
(c) O vetor velocidade média no intervalo do item ;
Ver solução completaUma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:
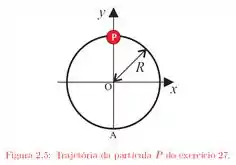
(d) A velocidade instantânea e a aceleração instantânea para e .
Ver solução completaUm atleta corre em uma pista de corrida circular com uma velocidade de com uma aceleração radial de .
(a) Qual o raio da pista?
Ver solução completaUm atleta corre em uma pista de corrida circular com uma velocidade de com uma aceleração radial de .
(b) Quanto tempo o atleta leva para completar uma volta?
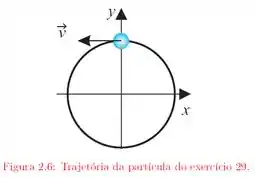
Ver solução completaUma partícula se desloca, no sentido anti-horário, sobre um círculo de raio , como mostra a figura . Sua velocidade escalar é descrita pela equação . Determine o módulo do vetor aceleração e o ângulo que esse vetor faz com o eixo quando , sabendo que nesse instante a partícula encontra-se na posição indicada na figura .
A hélice de um ventilador completa rotações em cada minuto. Considere um ponto localizado na extremidade da hélice que tem um raio de .
(a) Qual a distância percorrida por este ponto em uma volta?
Ver solução completaA hélice de um ventilador completa rotações em cada minuto. Considere um ponto localizado na extremidade da hélice que tem um raio de .
(b) Qual a sua velocidade e aceleração?
Ver solução completaUm corpo inicialmente em repouso, é acelerado em uma trajetória circular de raio , segundo a equação . Sabe-se que a partícula passa pela posição em . Determinar:
(a) A velocidade angular do corpo em função do tempo;
Ver solução completaUm corpo inicialmente em repouso, é acelerado em uma trajetória circular de raio , segundo a equação . Sabe-se que a partícula passa pela posição em . Determinar:
(b) A posição angular do corpo em função do tempo;
Ver solução completaUm corpo inicialmente em repouso, é acelerado em uma trajetória circular de raio , segundo a equação . Sabe-se que a partícula passa pela posição em . Determinar:
(c) As componentes tangencial e centrípeta de sua aceleração.
Ver solução completaUm bloco de massa está apoiado sobre outro bloco de massa , o qual está sobre uma mesa horizontal de massa .
(a) Indique todas as forças que agem em cada um dos blocos e na mesa;
Ver solução completaUm bloco de massa está apoiado sobre outro bloco de massa , o qual está sobre uma mesa horizontal de massa .
(b) Indique separadamente os pares de forças que correspondem que correspondem à ação e reação (3ª Lei de Newton);
Ver solução completaUm bloco de massa está apoiado sobre outro bloco de massa , o qual está sobre uma mesa horizontal de massa .
(c) Se invertemos as posições das massas, quais forças serão alteradas?
Ver solução completaUm bloco de massa é puxado ao longo de uma superfície, lisa e horizontal, por uma corda de massa sobre a qual se exerce uma força horizontal . Determine as acelerações do bloco e da corda e a força exercida pela corda sobre o bloco. Qual é o valor de se desprezarmos em confronto com ?
Ver solução completa36. Um bloco de está parado sobre um plano inclinado, devido ao atrito. Qual a componente da força que aplica no plano inclinado:
(a) Perpendicular à superfície e tangente à superfície?
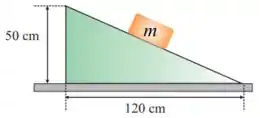
36. Um bloco de está parado sobre um plano inclinado, devido ao atrito. Qual a componente da força que aplica no plano inclinado:
(b) Qual o módulo, direção e sentido da força que o plano inclinado aplica em ?
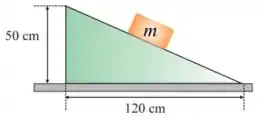
37. Um corpo de massa está apoiado em um plano liso de inclinação , o qual tem uma aceleração que mantém o corpo estacionário em relação ao plano, como mostra a figura 2.10. Determinar esta aceleração. O que acontecerá se o plano tiver uma aceleração com módulo maior que o valor encontrado?

38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(a) Quanto marcará a balança se o elevador estiver em repouso ou em movimento retilíneo e uniforme?
Ver solução completa38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(c) Quanto marcaria a balança se o cabo se rompesse, fazendo com que o elevador se precipitasse em queda livre?
Ver solução completa38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(d) O que ocorreria se o elevador fosse puxado para baixo com uma aceleração de ?
Ver solução completaTrês blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema da figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
(a) Considere , ou seja, que as massas e são iguais. Determine:
i) A razão entre as acelerações das massas e ;
ii) A aceleração de ;
iii) A tensão no fio.
Ver solução completaTrês blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema da figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
(c) A aceleração de cada bloco e a tensão na corda se e .
Ver solução completa40. Uma caixa de está sobre uma mesa horizontal. Os coeficientes de atrito estático e cinético, entre a caixa e a mesa, são e . A caixa é tracionada por um cabo que faz um ângulo com a horizontal. Determine a força de atrito e a aceleração da caixa se a tensão no fio for: (a) ; (b) .
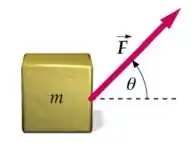
Um corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .
a) Sendo sem atrito a superfície entre os dois corpos, determinar a aceleração de cada um deles;
Ver solução completaUm corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .
b) Admitindo que a superfície entre os corpos seja suficientemente grosseira para que não escorre sobre , determinar a aceleração dos dois corpos;
Ver solução completaUm corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .
c) Determinar a força resultante que age sobre cada corpo em (b);
Ver solução completa38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(b) Quanto marcará a balança se o elevador tiver uma aceleração:
i. dirigida para cima e de módulo ?
ii. dirigida para baixo e de módulo ?
Ver solução completaA velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
a) Calcular a aceleração média no intervalo que se inicia em e termina em
Ver solução completaA velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
b) Determinar a expressão para e fazer os gráficos de e ;
Ver solução completaA velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
c) Determine (posição da partícula em função do tempo) por integração e use este resultado para determinar seu deslocamento durante o intervalo até . Qual a velocidade média neste intervalo de tempo?
Ver solução completaA velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
d) Qual a distância percorrida no intervalo de tempo ?
Ver solução completaUm motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.
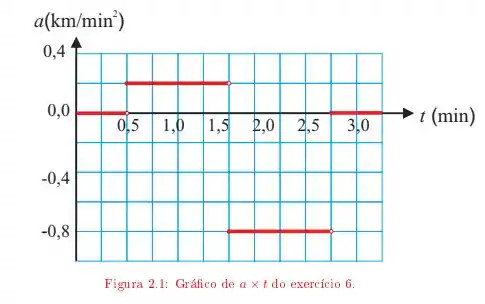
a) Faça o gráfico da velocidade para
Ver solução completaUm motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.
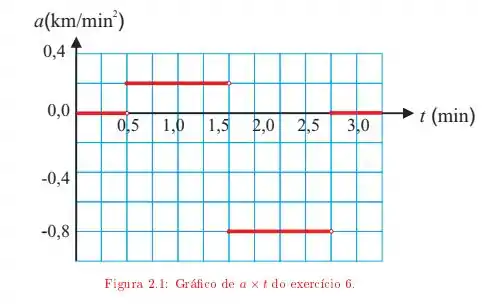
b) Determine a distância total percorrida pelo carro para este intervalo de tempo;
Ver solução completaUm motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.
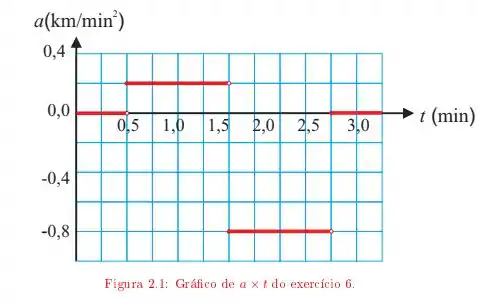
Determine o comprimento da rua.
Ver solução completaO gráfico da velocidade em função do tempo para uma partícula que sai da origem e se move ao longo do eixo está representado na figura .
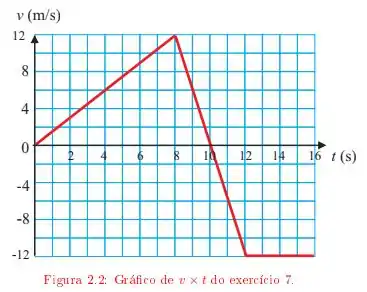
a) Trace os gráficos da aceleração instantânea e da posição para o intervalo de tempo
Ver solução completaO gráfico da velocidade em função do tempo para uma partícula que sai da origem e se move ao longo do eixo está representado na figura .
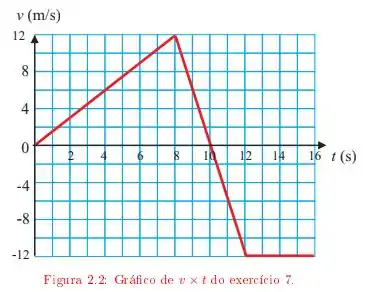
b) Quantos metros a partícula terá percorrido ao todo, para frente e para trás, no fim de segundos? Qual é o valor de neste instante?
Ver solução completaO gráfico da velocidade em função do tempo para uma partícula que sai da origem e se move ao longo do eixo está representado na figura .
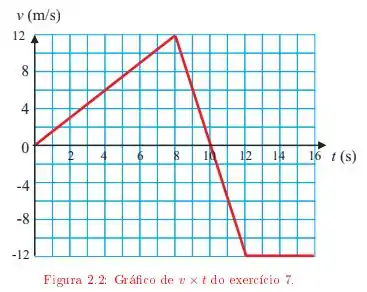
c) Qual o valor de em O que isso significa?
Ver solução completaUm objeto é abandonado, em , do alto de um prédio de de altura. Sua velocidade é dada por
a) Usando o processo de integração, calcule o deslocamento do objeto para . Quando vale .
Ver solução completaUm objeto é abandonado, em , do alto de um prédio de de altura. Sua velocidade é dada por
Calcule o deslocamento do objeto para ;
Ver solução completaUm objeto é abandonado, em , do alto de um prédio de de altura. Sua velocidade é dada por
c) Faça o gráfico de e calcule graficamente o deslocamento do objeto para , indicando as áreas que foram calculadas.
Ver solução completaUm trem parte de uma estação com aceleração constante de Um passageiro chega à estação segundos depois de o trem ter passado pelo mesmo ponto da plataforma. Qual é a menor velocidade constante que o passageiro deve correr para pegar o trem?
Resolva o problema de duas maneiras:
a) Analiticamente;
Ver solução completaUm trem parte de uma estação com aceleração constante de Um passageiro chega à estação segundos depois de o trem ter passado pelo mesmo ponto da plataforma. Qual é a menor velocidade constante que o passageiro deve correr para pegar o trem?
Resolva o problema de duas maneiras:
b) graficamente;
Ver solução completaDuas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrito pelas funções posição , e , onde a posição é medida em metros e o tempo em segundos.
a) Determine os vetores posição e de cada partícula e o vetor posição relativa , em termos dos vetores unitários e .
Ver solução completaDuas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrito pelas funções posição , e , onde a posição é medida em metros e o tempo em segundos.
b) Para , faça um esquema no plano cartesiano dos vetores , e Calcule a distância entre as partículas.
Ver solução completaDuas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrito pelas funções posição , e , onde a posição é medida em metros e o tempo em segundos.
c) Determine em que instante(s) as duas partículas colidem.
Ver solução completaDuas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrito pelas funções posição , e , onde a posição é medida em metros e o tempo em segundos.
d) Determine a velocidade relativa no(s) instantes no(s) qual(is) as partículas colidem.
Ver solução completaUma pedra, que se encontra numa elevação de sobre uma plataforma horizontal, é arrastada com velocidade de . A que distância horizontal do ponto de projeção ela atinge o solo? Qual é seu vetor velocidade neste instante?
Ver solução completaUma mangueira, com o bico localizado 1, 5 m acima do solo, é apontada para cima, segundo um ângulo de 30◦ com o chão. O jato de água atinge um canteiro a 15 m de distância.
a. Com que velocidade o jato sai da mangueira?
Ver solução completaUma mangueira, com o bico localizado 1, 5 m acima do solo, é apontada para cima, segundo um ângulo de 30◦ com o chão. O jato de água atinge um canteiro a 15 m de distância.
b. Que altura ele atinge??
Ver solução completaUma pedra cai de um balão que se desloca horizontalmente, com velocidade constante. A pedra permanece no ar durante 3 segundos e atinge o solo segundo uma direção que faz um ângulo de 30◦ com a vertical.
a. Qual é o vetor velocidade do balão?
Ver solução completaUma pedra cai de um balão que se desloca horizontalmente, com velocidade constante. A pedra permanece no ar durante 3 segundos e atinge o solo segundo uma direção que faz um ângulo de 30◦ com a vertical.
b. De que altura caiu a pedra?
Ver solução completaUma pedra cai de um balão que se desloca horizontalmente, com velocidade constante. A pedra permanece no ar durante 3 segundos e atinge o solo segundo uma direção que faz um ângulo de 30◦ com a vertical.
c. Que distância a pedra percorreu na horizontal?
Ver solução completaUma pedra cai de um balão que se desloca horizontalmente, com velocidade constante. A pedra permanece no ar durante 3 segundos e atinge o solo segundo uma direção que faz um ângulo de 30◦ com a vertical.
d. Qual o vetor velocidade da pedra quando atinge o solo?
Ver solução completaUm avião bombardeiro, a de altitude, voa em perseguição a um carro, no solo, que viaja a . Em dado instante, o avião lança uma bomba com velocidade escalar igual a , fazendo um ângulo de 30◦ com a horizontal. A que distância horizontal do carro deve ser lançada a bomba para que acerte o alvo?
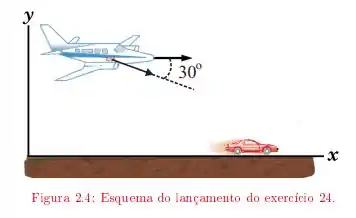
Uma bola, sob a ação apenas da aceleração da gravidade, é atirada do chão para o alto. Sabe-se que em uma altura de 9 m, sua velocidade, medida em m/s, é dada por. Calcule:
a. A altura que a bola subirá;
Ver solução completaUma bola, sob a ação apenas da aceleração da gravidade, é atirada do chão para o alto. Sabe-se que em uma altura de 9 m, sua velocidade, medida em m/s, é dada por. Calcule:
b. A distância horizontal percorrida pela bola;
Ver solução completaUma bola, sob a ação apenas da aceleração da gravidade, é atirada do chão para o alto. Sabe-se que em uma altura de 9 m, sua velocidade, medida em m/s, é dada por. Calcule:
c. O módulo da velocidade no ponto mais alto da trajetória;
Ver solução completaUma bola, sob a ação apenas da aceleração da gravidade, é atirada do chão para o alto. Sabe-se que em uma altura de 9 m, sua velocidade, medida em m/s, é dada por. Calcule:
d. O vetor velocidade no instante em que a bola volta a tocar o solo.
Ver solução completaUma vagão pode deslizar, sem atrito, sobre uma superfície horizontal. Um bloco , de massa , está encostado na face vertical do bagão, como mostra a figura . O coeficiente de atrito entre o bloco e o vagão é .
Determinar a aceleração mínima do vagão para que o bloco não caia;

Uma vagão pode deslizar, sem atrito, sobre uma superfície horizontal. Um bloco , de massa , está encostado na face vertical do bagão, como mostra a figura . O coeficiente de atrito entre o bloco e o vagão é .
Neste caso, qual é o módulo da força de atrito?

Uma vagão pode deslizar, sem atrito, sobre uma superfície horizontal. Um bloco , de massa , está encostado na face vertical do bagão, como mostra a figura . O coeficiente de atrito entre o bloco e o vagão é .
Sendo a aceleração maior que este mínimo, a força de atrito será maior que a calculada na parte ? Explique.

No esquema mostrado na figura , o carrinho de massa pode deslizar sem atrito, enquanto os coeficientes de atrito entre e a superfície horizontal valem e e .
Qual deve ser o menor valor de para que se inicie o movimento?
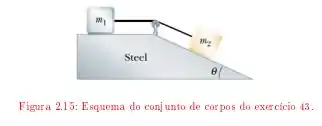
No esquema mostrado na figura , o carrinho de massa pode deslizar sem atrito, enquanto os coeficientes de atrito entre e a superfície horizontal valem e e .
Qual será a tensão na corda se e ?
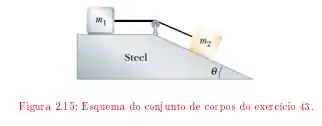
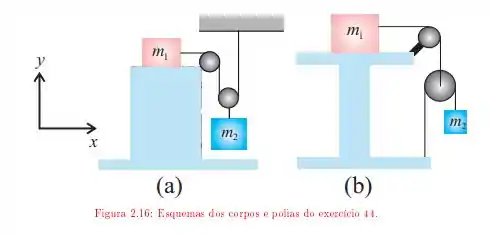
Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
O valor máximo da relação de modo que o sistema permaneça em equilíbrio;
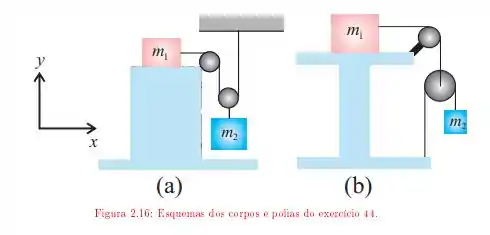
Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
A aceleração da massa quando:
Figura e ;
Figura e ;
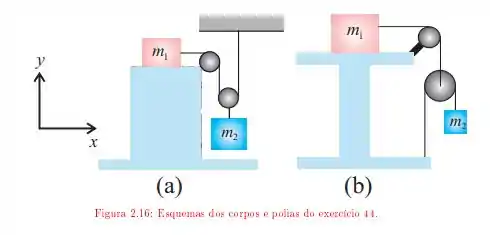
Os esquemas de corpos e polias na figura mostram sistemas constituídos por blocos de massas e e roldanas ideais, uma fixa e a outra móvel, pelas quais passam fios inextensíveis. As massas das roldanas e dos fios são desprezíveis comparadas às dos blocos. O bloco está apoiado em uma mesa e os coeficientes de atrito entre eles valem e . Para cada um dos esquemas, determine:
O vetor força que a haste, que suporta a roldana fixa, exerce sobre a mesa, em termos dos versores cartesianos e .
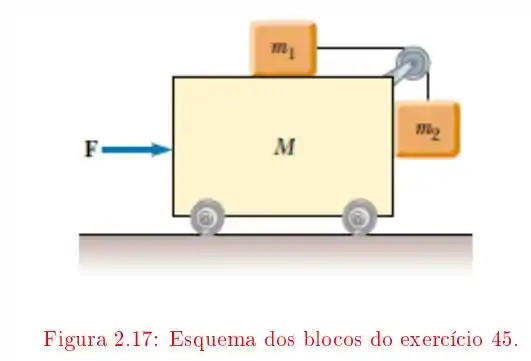
Na figura , os blocos estão ligados por fio e roldana ideais e podem deslizar sem atrito sobre as paredes do carrinho de massa . Qual o valor da força, aplicada ao carrinho, a partir do repouso, que faz com que fique parado em relação a ?
Um cubinho de gelo escorrega sobre um plano inclinado de inclinação no dobro do tempo que leva para escorregar em um plano análogo, mas sem atrito. Qual é o valor do coeficiente de atrito cinético entre o gelo e o plano?
Ver solução completaUm bloco desliza, para baixo, sobre um plano de inclinação , com velocidade constante. Ao atingir o final do plano, ele é projetado plano acima, por um dispositivo, com velocidade inicial . A aceleração da gravidade é .
Que distância acima, no plano, ele percorrerá, antes de parar?
Ver solução completaUm bloco desliza, para baixo, sobre um plano de inclinação , com velocidade constante. Ao atingir o final do plano, ele é projetado plano acima, por um dispositivo, com velocidade inicial . A aceleração da gravidade é .
Ele tornará a deslizar para baixo no plano inclinado? Explique.
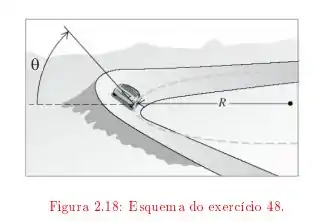
Ver solução completaUm carro trafega sobre uma estrada horizontal, na forma de um círculo de raio igual a . Sabendo que o coeficiente de atrito estático é , com que velocidade o carro pode trafegar sem risco de derrapar? SE a curva não for horizontal, mas inclinada, achar o ângulo de inclinação para que o carro a possa fazer a curva na ausência de atrito no pavimento.
Um estudante em um laboratório levanta uma rocha de massa m = 12 kg, e eleva-a, com aceleração desprezível, até a altura D = 1, 8 m, para colocá-la em um armário.
- Qual o trabalho realizado pelo estudante sobre a rocha?
Um estudante em um laboratório levanta uma rocha de massa , e eleva-a, com aceleração desprezível, até a altura , para colocá-la em um armário.
b. Qual o trabalho realizado pela força de atração gravitacional da Terra sobre a rocha?
Ver solução completaUm estudante em um laboratório levanta uma rocha de massa , e eleva-a, com aceleração desprezível, até a altura , para colocá-la em um armário.
b. Qual o trabalho realizado pela força de atração gravitacional da Terra sobre a rocha?
Ver solução completaUm funcionário empurra, num assoalho áspero, uma escrivaninha, cuja massa é igual a , com velocidade constante, por uma distância de . O coeficiente de atrito entre a mesa e o assoalho é de .
a. Qual o trabalho realizado pelo funcionário sobre a escrivaninha?
Ver solução completaUm funcionário empurra, num assoalho áspero, uma escrivaninha, cuja massa é igual a , com velocidade constante, por uma distância de . O coeficiente de atrito entre a mesa e o assoalho é de .
b. Qual o trabalho realizado pela força peso, pela força normal e pela força de atrito?
Ver solução completaUm funcionário empurra, num assoalho áspero, uma escrivaninha, cuja massa é igual a , com velocidade constante, por uma distância de . O coeficiente de atrito entre a mesa e o assoalho é de .
c. Qual o trabalho realizado sobre a escrivaninha por todas as forças que atuam sobre ela?
Ver solução completaUm engradado de massa é puxado com velocidade constante por um guincho, numa distância , numa rampa sem atrito, até uma altura acima do ponto de partida.
a. Qual é o módulo da força exercida pelo guincho e qual o trabalho realizado por esta força?
Ver solução completaUm engradado de massa é puxado com velocidade constante por um guincho, numa distância , numa rampa sem atrito, até uma altura acima do ponto de partida.
b. Quanto trabalho seria necessário para elevar o engradado verticalmente para cima, na mesma altura H? Neste caso, qual a força exercida pelo guincho?
Ver solução completaUm engradado de massa é puxado com velocidade constante por um guincho, numa distância , numa rampa sem atrito, até uma altura acima do ponto de partida.
c. Compare e analise os resultados encontrados nos itens anteriores.
Ver solução completaUm corpo de está em repouso sobre uma superfície horizontal, sem atrito. Uma força de módulo constante de , fazendo um ângulo de 30◦ com a horizontal, puxa o corpo. Determinar o trabalho efetuado pela força da corda e a velocidade escalar final do corpo, depois de deslocar-se sobre a superfície horizontal.
Ver solução completaUm bloco de está apoiado sobre uma mesa e ligado a uma mola horizontal que obedece a lei de Hooke , onde se mede a partir do comprimento de equilíbrio da mola e a constante de força vale . A mola está comprimida até .
a) Determinar o trabalho efetuado pela mola quando o bloco se desloca desde até a sua posição de equilíbrio , admitindo que não haja atrito entre o bloco e a mesa;
Ver solução completaUm bloco de está apoiado sobre uma mesa e ligado a uma mola horizontal que obedece a lei de Hooke , onde se mede a partir do comprimento de equilíbrio da mola e a constante de força vale . A mola está comprimida até .
b) Determinar a velocidade escalar do bloco em , admitindo que não haja atrito entre o bloco e a mesa;
Ver solução completaUm bloco de está apoiado sobre uma mesa e ligado a uma mola horizontal que obedece a lei de Hooke , onde se mede a partir do comprimento de equilíbrio da mola e a constante de força vale . A mola está comprimida até .
c) Determinar a velocidade escalar do bloco quando a mola está na posição de equilíbrio, mas agora admitindo que o coeficiente de atrito cinético entre a mesa e o bloco é .
Ver solução completaUma partícula move-se, sob a ação da força , no plano . Calcule:
a) O trabalho realizado pela força ao longo do quadrado indicado na figura . O que você conclui sobre o caráter conservativo ou não de ?
Ver solução completaUma partícula de massa desloca-se ao longo de uma reta. Entre e , ela está sujeita à uma força representada no gráfico da figura . Calcule a velocidade da partícula depois de percorrer e , sabendo que sua velocidade para é de .
Ver solução completaNum parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
a) Desprezando o atrito do carrinho com o trilho, qual é o menor valor de necessário para permitir ao carrinho dar a volta completa?
Ver solução completaNum parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
b) Se o carrinho cai no trilho em um ponto rotulado por , quando ainda falta percorrer mais um ângulo para chegar até o topo . Calcule .
Ver solução completaNum parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
c) Que acontece com o carrinho para ?
Ver solução completaUma partícula de massa se move ao longo da direção sob o efeito da força .
a) Tomando , calcule a energia potencial da partícula.
Ver solução completaUma partícula de massa se move ao longo da direção sob o efeito da força .
b) Faça um gráfico de em função de para o intervalo de posições . Determine as posições de equilíbrio e discuta suas estabilidades.
Ver solução completaUma partícula de massa se move ao longo da direção sob o efeito da força .
c) Considere o caso em que a partícula parte da origem com velocidade nula. Discuta o movimento da partícula nesta situação. Qual será a velocidade máxima e em que ponto isso ocorrerá?
Ver solução completaUma partícula de massa se move ao longo da direção sob o efeito da força .
d) Para que valores da energia mecânica total a partícula poderá apresentar um comportamento oscilatório?
Ver solução completaUma partícula está submetida a uma força dada pela energia potencial .
a) Qual é a força a que ela está sujeita?
Ver solução completaUma partícula está submetida a uma força dada pela energia potencial .
b) Qual é a variação de energia cinética entre os pontos e ? Este resultado depende do caminho percorrido pela partícula? Justifique.
Ver solução completaUma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
a) Quais são os pontos ou as regiões de equilíbrio?
Ver solução completaUma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
b) Se a energia mecânica total for determine as regiões permitidas para o movimento da partícula;
Ver solução completaUma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
c) Determine a energia cinética da partícula em ;
Ver solução completaUma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
d) Determine o trabalho realizado pela força para deslocar o corpo desde até ;
Ver solução completaUma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
e) Se a partícula tem energia cinética nula quando posicionada em , qual é a energia mínima que deve ser fornecida para que ela possa atingir a posição ? Neste caso, qual sua energia cinética em ?
Ver solução completaUma partícula de massa move-se em uma trajetória retilínea sob a ação de uma força conservativa , onde é medido em metros e em Newtons.
a) Determine a expressão da energia potencial associada a esta força, a qual satisfaz a condição .
Ver solução completaUma partícula de massa move-se em uma trajetória retilínea sob a ação de uma força conservativa , onde é medido em metros e em Newtons.
b) Esboce o gráfico de ;
Ver solução completaUma partícula de massa move-se em uma trajetória retilínea sob a ação de uma força conservativa , onde é medido em metros e em Newtons.
c) É possível essa partícula ter uma energia mecânica total igual a ? Justifique.
Ver solução completaUma partícula de massa move-se em uma trajetória retilínea sob a ação de uma força conservativa , onde é medido em metros e em Newtons.
d) Supondo que a partícula parta da origem com velocidade , encontre a energia mecânica total da partícula. Nesse caso seu movimento é oscilatório? Se sim, encontre os pontos de retorno clássico.
Ver solução completaA posição de uma partícula de massa é dada pela expressão onde é dado em metros e em segundos. Obtenha o trabalho realizado, durante os primeiros , pela força que atua sobre a partícula.
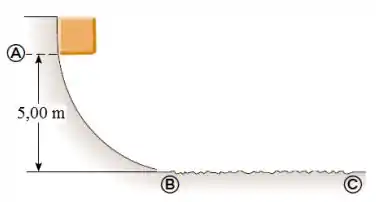
Ver solução completaUm carrinho desliza, a partir do repouso, do alto de uma montanha russa de de altura, com atrito desprezível. Chegando ao sopé da montanha, ele é freado pelo terreno coberto de areia, parando em . Qual é o coeficiente de atrito cinético entre o carrinho e a areia?
A corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
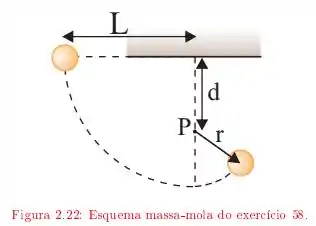
quanto está passando pelo ponto mais baixo da trajetória?
Ver solução completaA corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
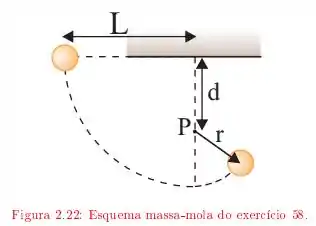
quando chega ao ponto mais alto da trajetória depois que a corda toca o pino?
Ver solução completaA corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
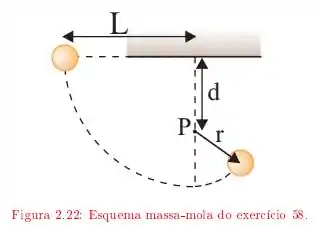
Mostre que para que a bola faça uma volta completa em torno do pino (Sugestão: A bola ainda deve estar se movendo quando chegar ao ponto mais alto da trajetória).
Ver solução completaUm bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .
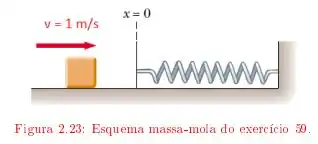
Qual é a deformação máxima da mola?
Ver solução completaUm bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .
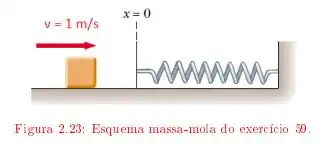
Que acontece depois que a mola atinge a sua deformação máxima?
Ver solução completaUm bloco de massa deslizando sobre uma mesa horizontal, com coeficiente de atrito cinético colide com uma mola de massa desprezível, de constante de mola inicialmente na posição relaxada. O bloco atinge a mola com velocidade de .
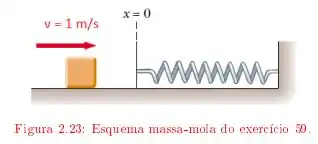
c) Que fração da energia inicial é dissipada pelo atrito nesse processo?
Ver solução completaUm vagão de massa está sobre um plano inclinado de inclinação , ligado a uma esfera suspensa, de massa , pelo sistema de cabos e polias ideais, como ilustrado na figura O coeficiente de atrito cinético entre o vagão e o plano inclinado é e o sistema é solto do repouso.
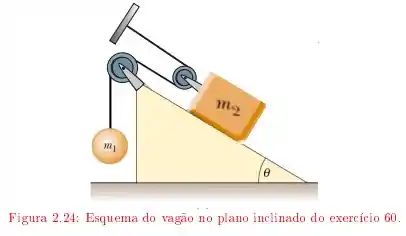
a) Determinar as relações entre os deslocamentos e as velocidades das massas e ;
Ver solução completaUm vagão de massa está sobre um plano inclinado de inclinação , ligado a uma esfera suspensa, de massa , pelo sistema de cabos e polias ideais, como ilustrado na figura O coeficiente de atrito cinético entre o vagão e o plano inclinado é e o sistema é solto do repouso.
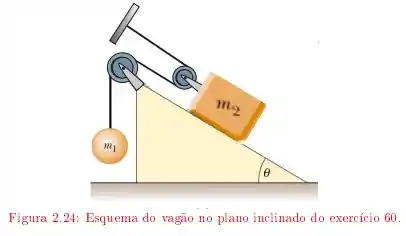
b) Utilizando a conservação da energia, calcule de que distância o vagão terá se deslocado, ao longo do plano inclinado, quando sua velocidade atingir
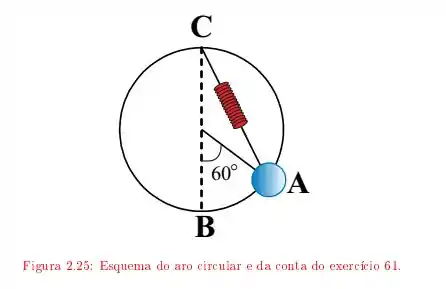
Ver solução completaUma conta de massa enfiada em um aro circular de raio situado em um plano vertical, está presa por uma mola de constante de mola ao ponto , localizado no topo do aro. Na posição relaxada da mola, ela está localizada em , o qual é o ponto mais baixo do aro. Se soltarmos a conta, a partir do repouso, do ponto , que faz um ângulo de com , como indicado na figura , com que velocidade ela atinge o ponto ?
O cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola é . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
A velocidade de elevador imediatamente antes de atingir a mola;
Ver solução completaO cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola é . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
b) A deformação máxima da mola;
Ver solução completaO cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola é . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
A altura que o elevador subirá de volta, a partir da posição inicial da mola relaxada;
Ver solução completaUm bloco de massa é solto em repouso em um plano inclinado de em relação ao plano horizontal, com coeficiente de atrito cinético Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava relaxada, de acordo com o esquema mostrado na figura .

a) Qual é a compressão sofrida pela mola?
Ver solução completaUm bloco de massa é solto em repouso em um plano inclinado de em relação ao plano horizontal, com coeficiente de atrito cinético Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava relaxada, de acordo com o esquema mostrado na figura .

b) Qual é a energia dissipada pelo atrito durante o trajeto do bloco desde o alto do plano até a compressão máxima da mola? Que fração representa da variação total de energia potencial durante o trajeto?
Ver solução completaUm bloco de massa é solto em repouso em um plano inclinado de em relação ao plano horizontal, com coeficiente de atrito cinético Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava relaxada, de acordo com o esquema mostrado na figura .

c) Se o coeficiente de atrito estático com o plano é de , que acontece com o bloco logo após colidir com a mola?
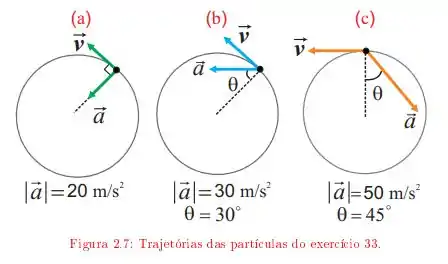
Ver solução completaNa figura podemos observar o movimento de três partículas, num certo instante . Todas elas deslocam-se no sentido anti-horário sobre círculos de raio , com velocidades variáveis (direção e/ou módulo). Nestes instantes aparecem, indicados nas figuras, também os vetores aceleração e seus módulos. Em cada um dos instantes assinalados na figura, achar os vetores velocidade e aceleração.
Três blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema na figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
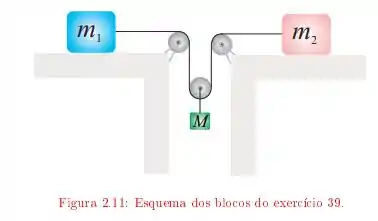
Suponha agora que as massas sejam todas diferentes. Determine
A relação entre as acelerações das massas , e ;
A aceleração de ;
A tensão no fio.
Ver solução completaUm corpo de massa , repousa sobre um outro de massa , que por sua vez está sobre uma superfície horizontal sem atrito. Uma força atua sobre conforme mostra a figura .

Qual é o módulo, a direção e o sentido da força de contato exercida pelo corpo de massa sobre o corpo de massa ?
Ver solução completaUma partícula move-se. sob a ação da força , no plano . Calcule:
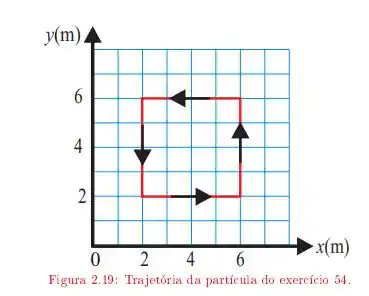
O trabalho realizado pela força ao longo da diagonal do quadrado da trajetória da figura , partindo da posição e chegando a posição .
O cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
A distância total, aproximada, percorrida pelo elevador antes de parar totalmente, utilizando, para isto, o princípio da conservação de energia. Porque esta resposta não é exata?
Ver solução completa