P-REC de Física 1 da USP - 2019

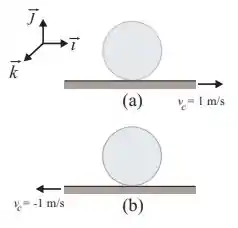
Um cilindro de raio rola sem deslizar com velocidade angular sobre uma correia móvel sob as condições mostradas na figura. No caso (a), a correia move-se com velocidade . No caso (b), a correia move-se com velocidade . Pode-se afirmar que as velocidades do centro do cilindro nos casos (a) e (b) são, respectivamente:

Uma partícula de massa move-se apenas sob a ação de uma força conservativa , onde é medido em metros e em Newtons. A variação da energia cinética da partícula quando ela se move da posição para a posição é:

(a)

(b)

(c)

(d)

(e)

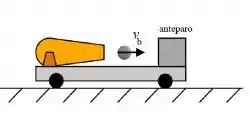
Um canhão é montado firmemente sobre um carrinho com rodas sem atrito, que está inicialmente em repouso em uma superfície horizontal lisa. O canhão dispara uma bala para a direita com uma velocidade , que é então capturada por um anteparo firmemente preso ao carrinho. Podemos afirmar que a velocidade final do sistema (constituído pelo carrinho+anteparo+canhão+bala) é:

1. , para a esquerda.
2. , para a direita.
3. .
4. , para a esquerda.
5. , para a direita.

Uma barra homogênea de comprimento é emendada a outra de mesmo comprimento, também homogênea, mas com o dobro da massa, conforme a figura.

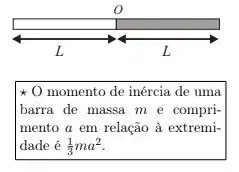
O símbolo na figura marca o ponto da emenda. Quando e representam as massas das barras, o momento de inércia e a distância do centro de massa do sistema em relação ao ponto de emenda valem, respectivamente:

Em um dado instante , observa-se que duas partículas de massas e estão nas posições e movendo-se com velocidades e , respectivamente. Passados , elas são novamente observadas e vê-se que encontra-se parada. Sabendo-se que elas estão sujeitas somente a forças internas, o vetor posição do centro de massa (em metros) quando é:

(a)

(b)

(c)

(d)

(e)

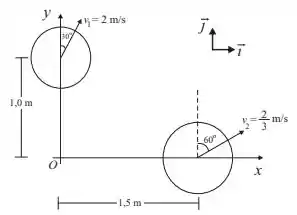
Dois objetos estão se movendo como mostra a figura ao lado. O objeto de massa move-se com vetor velocidade que faz um ângulo de com o eixo . O objeto de massa move-se com vetor velocidade que faz um ângulo de com o eixo . O valor do momento angular total em torno do ponto O é (no SI):