1º EE de Física 2 da UFPE - 2015.2

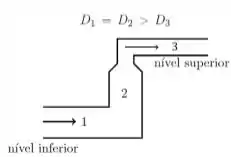
Para medir a massa de um planeta cujo raio é cinco vezes o raio da Terra, um astronauta deixa cair um objeto, a partir do repouso, a uma altura de 30 metros acima da superfície do planeta. Quando o objeto chega à superfície do planeta, sua velocidade é o dobro da velocidade que o objeto teria caso o mesmo experimento tivesse sido realizado na Terra. Qual é a massa desse planeta?

Na tubulação da figura ao lado, um fluxo estacionário de água passa de um nível mais baixo para um nível mais alto partindo da região 1 de diâmetro , passado pela região 2 de diâmetro e chegando à região 3 de diâmetro . Onde, . Sendo a pressão na região 1 e a velocidade do fluido na região 1, e assim por diante, marque a alternativa correta.

Um barco, inicialmente com uma âncora e um colete salva-vidas a bordo, flutua em uma piscina um pouco mais larga que o barco. Considere as seguintes situações: A âncora é jogada na piscina; A âncora é jogada fora da piscina; O colete salva-vidas é jogado na piscina. Responda o que acontece, respectivamente, com o nível da água nas situações descritas acima.

aumenta; diminui; diminui.

aumenta; diminui; permanece igual.

diminui; aumenta; permanece igual.

permanece igual; permanece igual; aumenta.

permanece igual; diminui; permanece igual.

aumenta; aumenta; permanece igual.

diminui; diminui; permanece igual.

aumenta; aumenta; aumenta.

diminui; diminui; diminui.

A figura ao lado mostra uma grande represa de água doce que tem uma profundidade . Um cano horizontal de de diâmetro é inserido a uma profundidade , como ilustrado ao lado. Uma rolha fecha a abertura do cano.

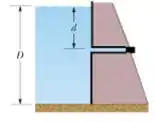
Determine o módulo da força de atrito entre a rolha e a parede do cano.

Quando a rolha é retirada, qual é o volume de água que sai do cano em 2 minutos? Use a equação de Bernoulli para obter esta resposta.

Uma partícula é lançada verticalmente a partir da superfície da Terra com velocidade de módulo . Ela atinge uma altura máxima em relação ao solo. Desprezando efeitos de atrito, determine .

Suponha um planeta de massa m segue uma órbita circular de raio e período ao redor de uma estrela de massa . Denotando por a constante gravitacional de Newton, calcule uma expressão para a razão em termos de e .

Considere um anel de raio e massa total cujo centro está a uma distância de uma partícula pontual de massa , conforme ilustrado na figura abaixo. Calcule a força gravitacional que age na partícula de massa , incluindo sua direção e sentido.

[Dica: Particione o anel em pequenos pedaços de massa infinitesimal e use argumentos de simetria para justificar que apenas uma componente da força é diferente de zero. Outra maneira de fazer o problema é calcular a energia potencial de interação e depois tomar a derivada em relação a .]

Dados: