A figura ao lado mostra uma grande represa de água doce que tem uma profundidade . Um cano horizontal de de diâmetro é inserido a uma profundidade , como ilustrado ao lado. Uma rolha fecha a abertura do cano.
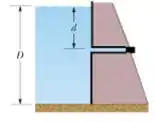
Determine o módulo da força de atrito entre a rolha e a parede do cano.
Quando a rolha é retirada, qual é o volume de água que sai do cano em 2 minutos? Use a equação de Bernoulli para obter esta resposta.
Passo 1
O liquido faz uma força na rolha e a força de atrito deve ser igual a essa força para que a rolha não voe e comece a vazar água.
Então nossa função é descobrir o valor da força , essa força é gerada pela pressão de água naquela extremidade do cano. Como a água está parada então podemos apenas calcular a pressão hidrostática. Bem essa pressão é dada pela altura.
Nesse caso então vamos substituir os valores, ; e
Agora que sabemos a pressão na rolha, podemos descobrir a força, lembrando que:
A área do cano é
Então a força na rolha será de
Aproximando, temos que
Passo 2
Para calcular o volume de água que sai em dois minutos, vamos usar a fórmula da Vazão
Bem, a área a gente tem e o tempo também, então só falta termos a velocidade da água quando sai e para isso usaremos como auxilio a equação de Bernoulli
Escolhendo os estados como estado 1 a partícula de água na superfície do reservatório e o estado 2 a partícula em contato com a rolha.
No estado 1 a pressão é a atmosférica a velocidade zero e a altura zero. Já no estado 2 a velocidade é o que eu quero, a altura é e a pressão também será a atmosférica pois a água está saindo (contato com o ar).
Passo 3
Agora que temos a velocidade basta substituir na formula que vimos no inicio para calcular o volume
A área já vimos que vale e o tempo é .
Resposta