Uma partícula é lançada verticalmente a partir da superfície da Terra com velocidade de módulo . Ela atinge uma altura máxima em relação ao solo. Desprezando efeitos de atrito, determine .
Suponha um planeta de massa m segue uma órbita circular de raio e período ao redor de uma estrela de massa . Denotando por a constante gravitacional de Newton, calcule uma expressão para a razão em termos de e .
Considere um anel de raio e massa total cujo centro está a uma distância de uma partícula pontual de massa , conforme ilustrado na figura abaixo. Calcule a força gravitacional que age na partícula de massa , incluindo sua direção e sentido.
[Dica: Particione o anel em pequenos pedaços de massa infinitesimal e use argumentos de simetria para justificar que apenas uma componente da força é diferente de zero. Outra maneira de fazer o problema é calcular a energia potencial de interação e depois tomar a derivada em relação a .]
Dados:
Passo 1
Como a altura máxima alcançada pela partícula é muito grande não podemos considerar a aceleração da gravidade constante e por isso não podemos usar as equações que aprendemos em física 1.
Para resolver essa questão precisamos usar o conceito de conservação de energia cinética que vimos em Gravitação.
A energia mecânica inicial é composta pela energia cinética inicial e energia potencial inicial, o valor da energia cinética nesse momento é:
Já o da energia potencial depende do raio do da Terra e será dado por:
Assim, a energia mecânica inicial é
Beleza, agora vamos calcular a energia mecânica final. No momento final a velocidade é zero, assim a energia cinética é zero também. Então a energia mecânica final é igual a energia potencial final.
Pela conservação de energia temos que
Agora, vamos substituir os valores que temos, pois foi dado pela prova
Passo 2
Em um movimento circular a força gravitacional será igual a força centrípeta.
Como queremos achar algo pelo período vamos substituir a velocidade por , pois a velocidade angular é , assim a força centrípeta é igual a
Igualando as forças temos
Queremos a razão
Então vamos isolar essa razão e assim obtemos:
Passo 3
Agora as coisas ficam um pouco mais delicadas. O que o problema nos descreve é isso:
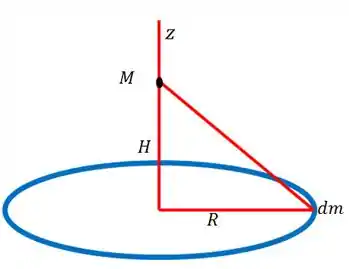
Bem, vamos seguir a dica dele então. Vamos provar que só terá força resultante diferente de zero no eixo . Bem, isso por que é um disco circular. Concorda que a partícula do disco de massa representada na figura acima gera uma força que terá componentes no eixo . Mas uma outra partícula do outro lado do irá gerar uma força igual, porem com o sentido oposto no eixo e mesmo sentido em . Assim, devido a simetria da figura as forças no plano irão se somar e dar uma resultante igual a zero. Pois a distância sempre será a mesma. Enquanto isso elas se somarão formará uma força no eixo .
Pela equação de força temos que a força gerada pela partícula do disco de massa , será:
Vamos começar a descobrir o que não temos a distância é a hipotenusa do triangulo retângulo, assim vale:
Então a força causada pela partícula é:
Mas essa é a força resultante, como vimos pela simetria a componente em não nos interessa, pois será cancelada, queremos apenas a força em , então vamos decompor essa força.
Para decompor temos que imaginar um ângulo, o mais fácil é o ângulo que a força faz com a horizontal,
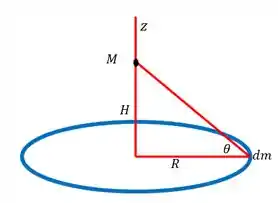
Sendo assim para encontrarmos a componente na direção , temos que multiplicar a força por , sendo o ângulo dentro do triangulo, podemos dizer que:
Assim a força causada por esse ponto infinitesimal é:
Agora para descobrirmos a força gerada por todo anel, basta integrarmos os dois lados dessa equação
A integral é o somatório de todas as massas infinitesimais do anel, o enunciado nos disse que a massa do anel é , assim:
Resposta