2º EE de Física 2 da UFPE - 2014.2

Cinco osciladores massa-mola, numerados de 1 a 5, estão suspensos no teto de uma sala. Uma britadeira cuja frequência de operação é fura o teto desta sala, forçando as massas a oscilarem. Os osciladores possuem todos a mesma massa e as constantes de mola têm os valores ; ; e . O oscilador que deve ter a maior amplitude de oscilação devido à perturbação externa é o:

a) oscilador 1

b) oscilador 2

c) oscilador 3

d) oscilador 4

e ) oscilador 5.

Uma massa é presa a duas molas, ambas de constante elástica , conforme a figura abaixo. A coordenada mede o deslocamento da massa em relação à sua posição de equilíbrio, onde ambas as molas encontram-se relaxadas.

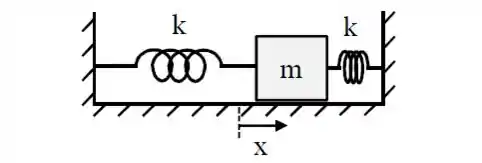
a)Use a segunda lei de Newton para obter a equação de movimento, que relaciona e

b) No instante a massa encontra-se em , com velocidade . Escrevendo a equação para o deslocamento instântaneo na forma determine os valores numéricos de .

c) Determine a energia total do sistema, nas condições do ítem (b).

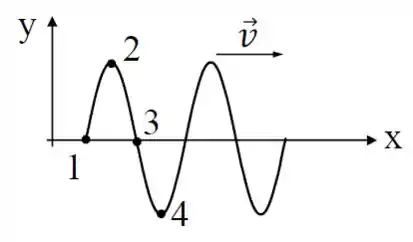
No instante a amplitude de uma onda transversal que propaga na direção de com velocidade é dada pelo gráfico abaixo. No sistema a equação que descreve a onda é:

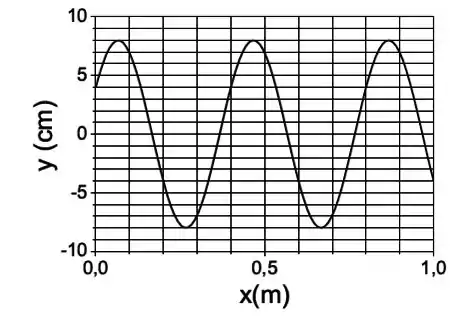
a)

b)

c)

d)

e)

Dois alto-falantes idênticos, separados por uma distância , emitem ondas sonoras de frequência e intensidade em direções opostas, conforme mostra a figura abaixo. Considerando a velocidade do som e supondo que a intensidade de cada alto-falante é constante na região entre eles, podemos afirmar que as intensidades do som respectivas aos pontos A, B e C, indicados na figura são:

a)

b)

c) ;

d) ;

e) ;

f ) .

Dois carros viajam na mesma direção e sentido. O carro aproxima-se com velocidade de uma sirene estacionária, onde é a velocidade do som. O carro afasta-se da sirene, com a mesma velocidade Denotando por as frequências do som detectadas pelos carros , respectivamente, podemos afirmar que:

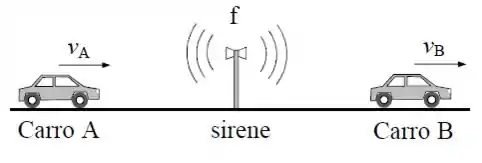
a)

b)

c)

d)

e)

Na figura abaixo a extremidade de uma corda é presa a um oscilador senoidal de frequência e a outra é presa a uma massa , passando por uma roldana. A massa específica da corda é e a amplitude do oscilador é suficientemente pequena para que o ponto possa ser considerado um nó.

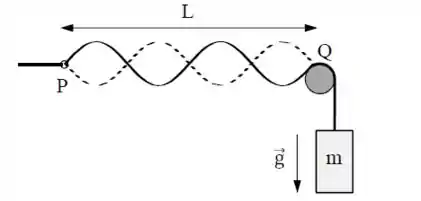
a) Qual deve ser a massa para que o oscilador produza uma oscilação no harmônico da corda? Expresse sua resposta em termos de

b) Nas condições do item (a) determine a ordem do harmônico se dobrarmos o comprimento da corda, mantendo tudo o mais inalterado.

A figura abaixo mostra uma onda transversal propagando numa corda tensionada com velocidade v no sentido de . Denotando por as velocidades tranversais dos pontos 1, 2, 3 e 4 da corda, podemos afirmar que:

a)

b)

c)

d)

e)