Na figura abaixo a extremidade de uma corda é presa a um oscilador senoidal de frequência e a outra é presa a uma massa , passando por uma roldana. A massa específica da corda é e a amplitude do oscilador é suficientemente pequena para que o ponto possa ser considerado um nó.
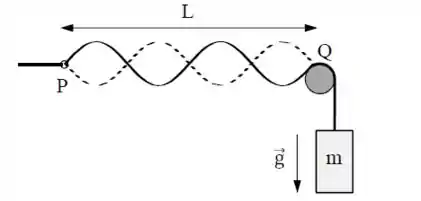
a) Qual deve ser a massa para que o oscilador produza uma oscilação no harmônico da corda? Expresse sua resposta em termos de
b) Nas condições do item (a) determine a ordem do harmônico se dobrarmos o comprimento da corda, mantendo tudo o mais inalterado.
Passo 1
a)
Primeiro vamos calcular a velocidade de propagação:
Onde a tensão é igual ao peso:
Assim:
A frequência de oscilação de cada harmônico é dada por:
Para temos . Assim:
Assim:
Passo 2
b)
De a):
Para o quarto harmônico.
Temos que:
O comprimento permanece constante, já que nenhuma das variáveis acima mudou.
Observação: a densidade da corda mudou com o aumento da corda? Você poderia pensar que sim, mas isso só aconteceria no caso em que a massa se mantivesse constante. Nada foi dito sobre isso, então, consideramos que
Assim, a nova relação, para o novo comprimento
Assim:
Assi, a onda vai oscilar no harmônico.
Resposta
a)
b)
harmônico