A figura abaixo mostra uma onda transversal propagando numa corda tensionada com velocidade v no sentido de . Denotando por as velocidades tranversais dos pontos 1, 2, 3 e 4 da corda, podemos afirmar que:
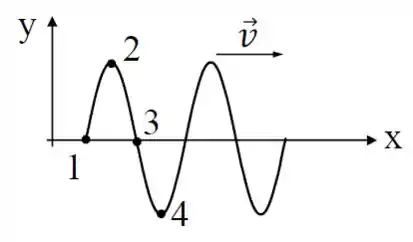
a)
b)
c)
d)
e)
Passo 1
Podemos analisar isso desenhando a onda alguns instantes depois do instante retratado na figura acima:
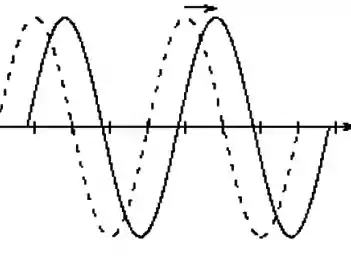
No caso da figura acima, o traço pontilhado mostra a onda no instante e o contínuo a onda alguns instantes depois.
Passo 2
Para o ponto 2, perceba que a altura não se altera:
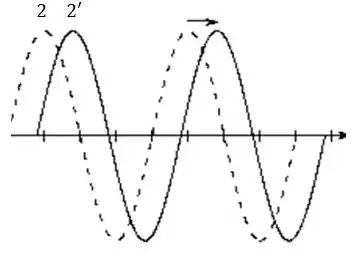
Assim:
Passo 3
Já o ponto 3 “sobe” com o passar da onda:
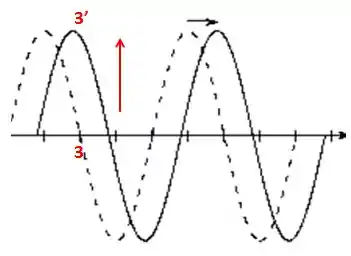
Assim:
Passo 4
E o ponto 1? Não dá pra analisa-lo com a figura que colocamos ali, pelo menos não diretamente. Porém, como a onda é um padrão repetitivo, podemos usar um ponto equivalente, logo mais a frente:
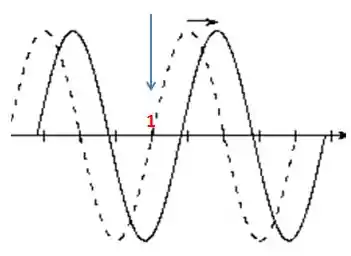
Assim, analisando esse ponto:
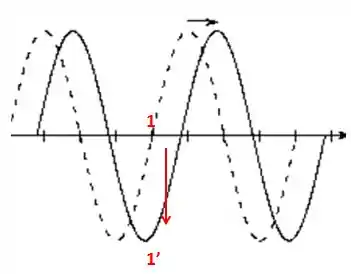
Percebemos que o ponto “desce”. Assim:
Passo 5
E o ponto Não precisamos nem pensar nele, afinal de contas, ele é um ponto de pico. Qual o outro ponto de pico que analisamos?
O ponto 2. Como vimos, a velocidade transversal desse ponto é nula, assim, a velocidade do ponto 4 também é nula:
Resposta
c)