Origem do Exercício
Uma massa é presa a duas molas, ambas de constante elástica , conforme a figura abaixo. A coordenada mede o deslocamento da massa em relação à sua posição de equilíbrio, onde ambas as molas encontram-se relaxadas.
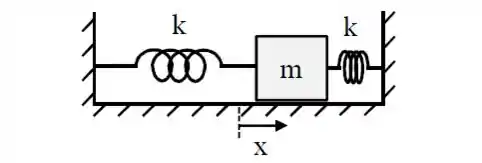
a)Use a segunda lei de Newton para obter a equação de movimento, que relaciona e
b) No instante a massa encontra-se em , com velocidade . Escrevendo a equação para o deslocamento instântaneo na forma determine os valores numéricos de .
c) Determine a energia total do sistema, nas condições do ítem (b).
Passo 1
a)
temos:
A força é elástica:
Além disso:
Assim:
Opa! Por que Porque são duas molas, quando uma é distendida em metros, a outra é comprimida em metros. Assim, a força fica duplicada.
Passo 2
b)
Pelo enunciado, sabemos que:
Da equação:
Assim:
Agora, usando a função do deslocamento e da velocidade em
E:
Para
Assim, jogando na primeira equação:
Logo:
Passo 3
A energia total é dada por:
Nas notações desse problema:
Porém, nesse caso, . Por fim:
Resposta
a)
b)
c)