P1 de Física 2 da UFRJ - 2013.2

Dois grandes recipientes, com temperaturas inicialmente distintas, devem ser colocados em contato térmico através de uma ponte metálica.

Para tal ponte, se dispõe dois cilindros de área e comprimento : um com condutividade térmica , o outro com .

São estudados os três casos abaixo, sempre colocando as bases dos cilindros em contato com os recipientes:

1. Só se usa um cilindro, o de condutividade menor.
2. Os dois cilindros lado a lado, mas sem encostar um no outro.
3. Os recipientes são afastados e coloca-se os dois cilindros em série (um após o outro).

Qual a ordenação correta para as taxas de condução de calor?

Considere os três processos abaixo, isolados do resto do universo.

(I) Um cubo de alumínio é colocado em um copo de água. Após algum tempo, o alumínio aumentou de tamanho e a água esfriou.

(II) Cera sólida é colocada no fundo de uma panela quente. Após algum tempo, a cera derreteu e a panela esquentou.

(III) Um motor converte em trabalho toda a energia térmica liberada pela fusão de gelo em água.

Quais destes processos violam, necessariamente, a Primeira Lei da Termodinâmica?

Considere os seguintes gases comuns em nossa atmosfera: nitrogênio, com , e oxigênio, com .

Suponha que estes gases estejam em condições de volume, temperatura e pressão nas quais possam ser considerados gases ideais.

Se os gases estão à mesma temperatura, então considere as seguintes afirmativas:

1. As moléculas destes gases possuem a mesma energia cinética translacional.
2. As moléculas de oxigênio são, em média, mais rápidas que as moléculas de nitrogênio.
3. O gás que possui as moléculas com a maior energia cinética translacional é o oxigênio, pois possui maior massa molar.

As CORRETAS são:

1. Apenas I.
2. Apenas II.
3. Apenas III.
4. Apenas I e II.
5. Apenas II e III.

Dadas as seguintes afirmativas a respeito de um gás ideal com calores específicos (a volume constante) e (a pressão constante):

1. É necessário fornecer uma quantidade de calor maior para um mesmo número de moles de um gás ideal a volume constante do que a pressão constante para que este gás sofra uma dada variação de temperatura.
2. A altas temperaturas, é necessário fornecer uma quantidade de calor menor para um mesmo número de moles de um gás ideal monoatômico do que um gás diatômico para que estes gases sofram uma mesma variação de temperatura.
3. Em um processo realizado a pressão constante, a variação de energia interna de um gás ideal só depende da quantidade de calor trocada com as vizinhanças.

As CORRETAS são:

1. Apenas I.
2. Apenas II.
3. Apenas III.
4. Apenas I e II.
5. Apenas II e III.
6. Apenas I e III.

A figura abaixo mostra três possíveis expansões de um gás ideal monoatômico, que encontra-se inicialmente no estado (cujo volume é ) para os estados finais , ou , todos de volume , através de três processos reversíveis diferentes:

I – transformação isobárica;

II – transformação isotérmica

III – transformação adiabática

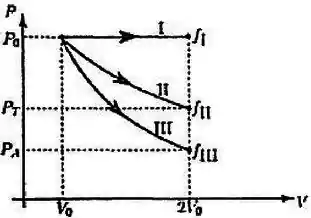
Sobre tais processos, é INCORRETO afirmar que:

1. A maior troca de calor se dá no processo isobárico.
2. O trabalho realizado pelo gás é menor no processo adiabático.
3. No processo isotérmico, todo o trabalho é transformado em calor.
4. As temperaturas finais terão a relação .
5. Na transformação isotérmica, não haverá calor trocado com o gás, uma vez que .

Colocamos uma forma cheia d’água à temperatura ambiente dentro do congelador, que está a uma temperatura .

Considere as seguintes afirmativas sobre tal processo:

1. O equilíbrio térmico será necessariamente atingido a .
2. Neste caso, o congelamento da água é um processo irreversível.
3. Durante a transição de fase, a temperatura da água não vai variar.

As afirmativas CORRETAS são:

1. Apenas I.
2. Apenas II.
3. Apenas III.
4. Apenas I e II.
5. Apenas I e III.
6. Apenas II e III.

Um mol de um gás ideal é submetido a um ciclo reversível consistindo de duas ADIABÁTICAS e duas ISÓCORAS, como mostra o diagrama - na figura.

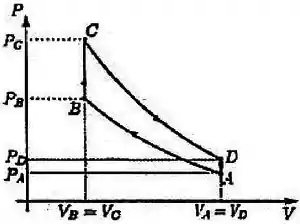
Marque a opção que melhor representa o MESMO ciclo em um diagrama -.

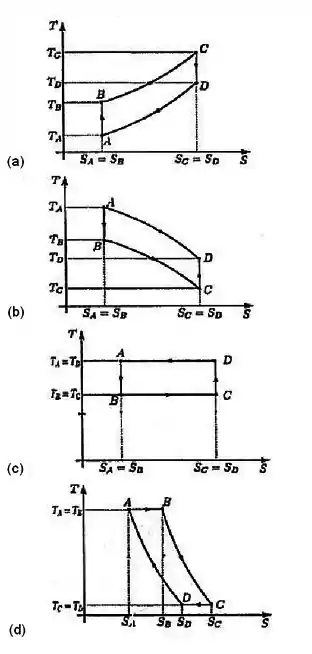
Um pesquisador quer estudar o comportamento termodinâmico de sólidos através de uma simulação de computador.

Ele modela um sólido como uma rede cristalina de de átomos ligados aos seus vizinhos por molas ideais.

Contudo, seus “átomos” estão restritos a um plano (ou seja, a simulação é inteiramente bidimensional).

Para testar se sua simulação está bem feita, ele calcula a energia interna do seu sólido.

Qual o valor que ele espera encontrar?