PF de Física 2 da UFRJ - 2016.1

Um corpo A, de massa m e calor específico c, a uma temperatura inicial TA troca calor com um reservatório térmico R a temperatura fixa TR, sem realizar ou sofrer trabalho. Se A muda sua temperatura para T’A, as variações de entropia em A, ∆SR são dadas por

(a) .

(b)

(c)

(d)

(e)

Das afirmações a seguir, quais delas são verdadeiras? (i) Em um gás ideal o módulo da velocidade das moléculas é inalterado imediatamente após elas colidirem com as paredes do recipiente que as contém. (ii) Num gás ideal não há energia potencial de interação entre as suas moléculas. (iii) A energia interna de um gás ideal é sempre diretamente proporcional à sua temperatura e inversamente proporcional à sua pressão.

(a) Apenas (i).

(b) Apenas (ii).

(c) Apenas (iii).

(d) Apenas (i) e (ii).

(e) Apenas (i) e (iii).

(f) Apenas (ii) e (iii).

(g) Todas elas.

(h) Nenhuma delas.

Uma onda harmônica viajando em uma corda é refletida em uma de suas extremidades. Sabendo que a onda refletida mantém a amplitude e a frequência da onda incidente, assinale a alternativa INCORRETA.

(a) A onda refletida transporta a mesma potência média que a onda incidente. Porém, ela transporta energia no sentido oposto.

(b) A onda refletida interferirá com a onda incidente, gerando uma onda estacionária.

(c) Se a extremidade da corda em questão for fixa, a interferência entre as ondas incidente e refletida será destrutiva nesta extremidade.

(d) As duas ondas encontram-se em fase na extremidade da corda em questão se ela for fixa.

(e) A potência transmitida pela combinação das ondas incidente e refletida é nula em média, mas não a cada ponto e instante.

Uma ambulância trafega em alta velocidade com a sirene ligada produzindo um som de frequência . Na rua há uma pessoa parada. Ele vê a ambulância aproximando-se com uma velocidade de . Se a velocidade do som nas condições locais de temperatura e pressão é de , a pessoa na rua percebe então uma frequência e o motorista da ambulância percebe a frequência , tem-se como correta a opção:

(a) ;

(b) ;

(c) ;

(d) ;

(e) ;

(f) .

Um tubo cilíndrico e de seção reta uniforme, tem suas extremidades abertas e em contato com o ar. Uma onda sonora no seu interior apresenta modos normais de vibração de frequências , onde . Ao fecharmos uma de suas extremidades com uma parede fixa, seus modos normais passam a ter frequências , onde . Qual a razão entre as frequências do n-ésimo modo normal de vibração nas duas situações, ? Quando esta razão se aproxima de 1?

(a) . Para frequências suficientemente baixas.

(b) . Para frequências suficientemente altas.

(c) . Para frequências suficientemente baixas.

(d) . Para frequências suficientemente altas.

(e) . Para nenhuma frequência.

Um bloco de massa está preso à extremidade inferior de uma mola ideal de constante elástica cujo extremo superior está preso ao teto por um suporte fixo e alinhada com a direção vertical. Um segundo bloco, também de massa , está ligado ao primeiro bloco por meio de um fio ideal. Inicialmente, o sistema encontra-se em equilíbrio, como mostra a figura.

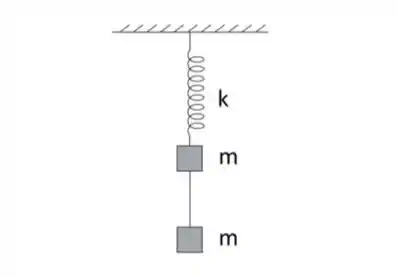
Em um dado instante, corta-se o fio e o sistema formado pela mola e pelo bloco preso em sua extremidade inferior começam a oscilar verticalmente. Supondo desprezíveis todos os atritos e sendo o módulo da aceleração da gravidade, assinale a opção que indica, respectivamente, o período e a amplitude das oscilações harmônicas executadas por esse bloco.

(a) e .

(b) e .

(c) e .

(d) e .

(e) e .

Considere um escoamento estacionário de um fluido numa canalização horizontal com área de seção reta constante, uma linha de corrente, também horizontal, e dois pontos distintos nesta linha, 1 e 2. Se a velocidade do fluido for a mesma nos dois pontos, marque a alternativa que relaciona corretamente a densidade e a pressão do fluido no ponto 1, e , à densidade e à pressão do fluido no ponto 2, e :

(a) > , > .

(b) > , = .

(c) ρ 2 , = .

(d) = , = .

(e) = , p 2 .

(f) = , > .

Dois gases ideais idênticos, e , de mesmo volume inicial , se expandem, aumentando seu volume de uma mesma quantidade . O gás expande-se livremente e em isolamento térmico, enquanto o gás expande-se lentamente, realizando trabalho e sem que sua temperatura varie. Julgue as seguintes alternativas:

I. O gás não realiza trabalho ao se expandir.

II. A variação de entropia é igual em ambos os casos.

III. O gás têm sua temperatura reduzida por conta da expansão.

IV. A variação de entropia em é maior do que a variação de entropia em .

V. A expansão de não causa o aumento de sua entropia, pois o processo é reversível.

(a) Apenas I está correta.

(b) Apenas II está correta.

(c) Apenas I e II estão corretas.

(d) Apenas I e V estão corretas.

(e) Apenas IV e V estão corretas.

(f) Apenas III e IV estão corretas.

(g) Apenas III, IV e V estão corretas.

Um gás está inicialmente em equilíbrio térmico com um reservatório térmico a temperatura . Ele pode realizar a mesma quantidade de trabalho de duas maneiras distintas, através de uma expansão isotérmica até atingir o volume ou através de uma expansão adiabática até atingir volume e temperatura . É correto afirmar que:

(a) e .

(b) e .

(c) e .

(d) e .

(e) e .

(f) e .

A figura mostra um bloco de massa que oscila sobre uma superfície horizontal, sem atrito, sob a ação de uma força elástica produzida por uma mola, da forma:

,

Onde indica a posição horizontal do bloco em um dado sistema de coordenadas, e são constantes e e .

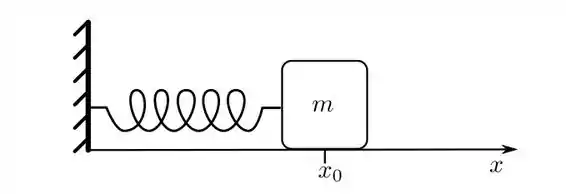
a) Qual a posição de equilíbrio do bloco, , tal que a mola encontra-se relaxada?

b) Encontre a equação diferencial de movimento para a posição do bloco.

c) Encontre a solução geral da equação encontrada no item anterior, sem impor condições iniciais.

d) Encontre a função horária se em o bloco está em e parte do repouso.

e) Esboce para as primeiras oscilações (decorridos dois períodos) do bloco, respeitando as condições do item . O bloco oscila em torno de que posição?

f) Determine a energia potencial elástica para este sistema. Esboce um gráfico para , indicando nele a posição de equilíbrio.