P2 de Física 2 da UFRJ - 2016.1

Uma onda progressiva em uma corda tem seu perfil de deslocamento descrito por onde é uma função em forma de pulso. Ela incide em uma extremidade fixa da corda em , sendo refletida. Sobre a onda refletida , é correto afirmar que

1. É descrita por e o pulso refletido volta sem defasagem.
2. É descrita por e o pulso refletido volta om defasagem de 180◦.
3. É descrita por e o pulso refletido volta com defasagem de 180◦.
4. É descrita por e o pulso refletido volta sem defasagem.
5. É descrita por e o pulso refletido volta sem defasagem.
6. É descrita por e o pulso refletido volta sem defasagem.

Observação: Acreditamos que existe um erro no enunciado. Usamos ,na resolução,

Um objeto de massa m se move no eixo sujeito a uma força horizontal de modo que a equação de movimento é dada por , onde ≥ 0, > 0 e > 0. A amplitude da solução particular desta equação varia com ω de acordo com o que mostra a figura em três situações correspondentes a valores diferentes e , tal que ≫ .

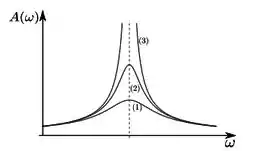
É INCORRETO afirmar que:

a) Quanto maior o valor de , maior a amplitude máxima da curva correspondente.

b) O amortecimento é maior na curva (1).

c) A frequência de ressonância é a mesma para as três curvas.

d) A curva (3) corresponde ao aso sem amortecimento.

e) Para ω ≫ , a solução particular é defasada de π em relação à força externa.

Uma corda está esticada e vibra com o padrão mostrado na figura. Se o seu comprimento natural é de e a tração do fio e a sua densidade linear , é correta a opção para o comprimento de onda λ e frequência :

1. ;
2. ;
3. ;
4. ;

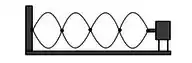
Uma corda de comprimento esticada tem uma extremidade mantida fixa () e a outra livre . Considere que, na configuração de equilíbrio, a corda se encontra na horizontal ao longo do eixo . Um aluno escreve que os pequenos deslocamentos transversais na direção podem ser representados pelos modos normais:

Onde = 1, 3, 5, ... , e são constantes a serem determinadas das condições iniciais do problema e é a velocidade de propagação da onda na corda. São feitas as seguintes observações sobre a solução apresentada:

1. Ela está incorreta, pois não obedece a condição de contorno .
2. Os modos pares com = 2, 4, 6,... também deveriam ter sido levados em consideração.
3. As condições de contorno para neste problema são as mesmas que uma onda sonora de deslocamento deve obedecer em um tubo de comprimento fechado em uma extremidade e aberto na outra.
4. Esta solução não representa uma solução da equação de onda, pois não pode ser escrita na forma, onde é uma constante real e e são funções de uma variável.

São verdadeiras:

1. Somente a (III).
2. Todas são verdadeiras.
3. Nenhuma é verdadeira.
4. Somente (I) e (II).
5. Somente (I) e (IV).
6. Somente (III) e (IV).
7. Somente (II) e (IV).
8. Somente a (IV)

Um objeto de massa m que pode se mover ao longo do eixo é sujeito a uma força do tipo . No instante de tempo inicial, ele se encontra na posição de equilíbrio em , e recebe um impulso de modo que sua velocidade inicial é > 0. O gráfico que melhor representa como a posição deste objeto varia om o tempo é:

a)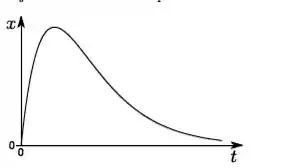

b)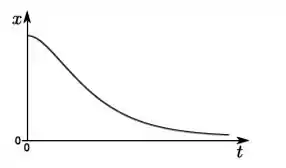

c)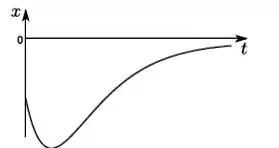

d)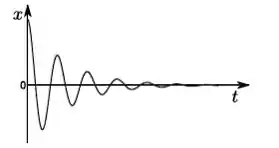

e)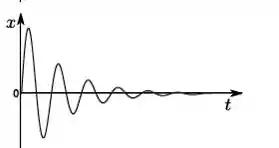

f)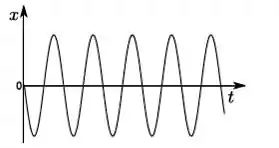

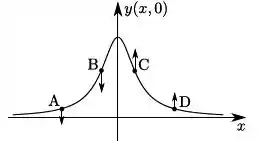
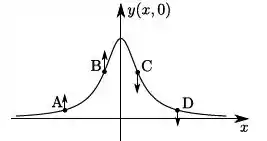
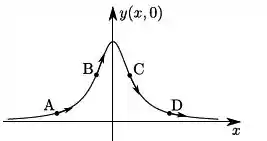
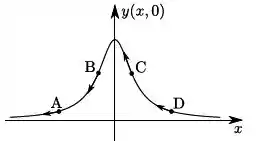
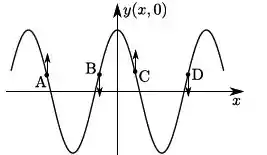
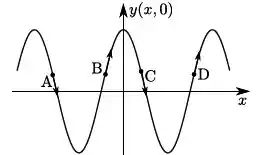
Uma corda muito longa é mantida tensa e, por ela, se propaga uma onda transversal, cujos deslocamentos verticais são dados por:

onde , e são constantes positivas. Considere que, no equilíbrio, a corda se encontra na horizontal ao longo do eixo . A figura que representa corretamente a configuração da corda no instante e as velocidades dos pontos , , e da corda é:

a)

b)

c)

d)

e)

f)

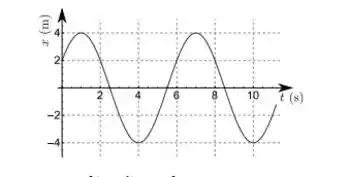
O gráfico a seguir mostra como a posição de um móvel oscila com o tempo . A lei horária da posição deste objeto é melhor descrita por

2. (

Um único sistema massa-mola é colocado para oscilar de três maneiras diferentes. No caso (A), o sistema está alinhado verticalmente, com uma extremidade da mola presa ao teto, no caso (B), horizontalmente com a massa deslocando-se sobre uma superfície sem atrito e finalmente no caso (C), em um plano inclinado de um ângulo , onde a massa desloca-se sobre a superfície também sem atrito. Denominado-se as frequências angulares para cada maneira como respectivamente, é correta a opção:

1. ;
3. ;
5. ;

Uma fonte sonora e um observador se movem com a velocidade vetorial em relação ao ar. A fonte emite um som contínuo de frequência e o observador detecta, para o mesmo som, uma frequência. Assinale a alternativa correta.

1. A velocidade relativa entre e é nula e a distân ia atravessada entre eles por cada frente de onda é constante. Portanto, .
2. A relação entre e depende do valor específico de , sendo possível que , ou .
3. O movimento da fonte não altera a frequência observada, portanto, como o observador se aproxima de , .
4. O movimento da fonte não altera a frequência observada, portanto, como o observador se aproxima de , .
5. O movimento do observador não altera a frequência observada, portanto, como a fonte se afasta .

Um pêndulo simples é formado por um fio ideal de comprimento , ligado a uma massa em uma extremidade e na outra presa a um pino na parede, de modo que ele pode girar livremente, como mostra a figura. Considere conhecida a aceleração da gravidade.

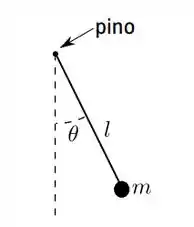
1. Mostre que a energia mecânica (energia cinética + potencial) E deste sistema pode ser escrita como:

Dica: Considere a energia potencial mínima igual a zero no ponto mais baixo da tra jetória do pêndulo.

2. Determine o valor da energia mecânica tal que para o movimento é ilimitado (isto é, o pêndulo pode completar uma volta completa).
3. Aplicando princípios de conservação da energia, obtenha a equação de movimento para as oscilações do pêndulo.
4. Obtenha o período do pêndulo na aproximação de ângulos pequenos (quando, ).
5. Encontre a solução para a equação de movimento deste pêndulo om a aproximação de ângulos pequenos para encontrar o ângulo θ como função do tempo . Considere que, no instante inicial , o pêndulo se encontra na posição de equilíbrio , mas recebe um impulso de modo que a sua velocidade angular inicial é , onde é um parâmetro adimensional conhecido.