P3 de Física 2 da UNICAMP - 2017.2 (diurno)

Uma massa de um metal tem sua temperatura aumentada até sua temperatura de fusão, por um forno de potência . Se a potência do forno é mantida por um tempo até que o metal se liquefaça, o calor latente de fusão do metal é dado por:

a)

b)

c)

d)

e)

O calor específico do chumbo é 0,03 cal/g. Se 1000 g de pequenas esferas de chumbo a 100 são misturados com 20 g de água (calor específico de 1 cal/(g)) a 70 em um recipiente termicamente isolado, a temperatura final da mistura é:

a) 88;

b) 85;

c) 80;

d) 90;

e) 95.

Se, quando a temperatura de uma moeda de cobre aumenta de 100 , o diâmetro da moeda aumenta de 0,17%, a área de uma das faces da moeda aumenta de:

a) 0,34%;

b) 0,17%;

c) 0,51%;

d) 0,13%;

e) 0,27%;

Se um gás se expande livremente no vácuo:

a) a expansão é adiabática, o trabalho realizado é zero, a energia interna do gás permanece a mesma e a temperatura do gás permanece a mesma;

b) a expansão é adiabática, o trabalho realizado é zero, a energia interna do gás diminui e a temperatura do gás diminui;

c) a variação de entropia é zero;

d) a expansão é adiabática, o gás realiza trabalho sobre o ambiente, e a energia interna do gás diminui;

e) a expansão ocorre a uma pressão constante;

Quando um sistema passa do estado i para o estado f seguindo a trajetória iaf no diagrama p-V da figura, Q = 50 cal e W = 20 cal. Ao longo da trajetória ibf Q = 36 cal. O trabalho W ao longo da trajetória ibf é:

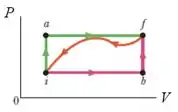
a) 6 cal;

b) – 6 cal;

c) 2 cal;

d) 12 cal;

e) 18 cal.

Considere um gás hipotético no qual as partículas constituintes podem ser encontradas com apenas 5 possíveis velocidades, de acordo com a tabela a seguir:

= 100 m/s : 3 partículas

= 140 m/s : 4 partículas

= 200 m/s : 7 partículas

= 230 m/s : 10 partículas

= 250 m/s : 6 partículas

A velocidade mais provável das partículas é:

a) 230m/s

b) 202 m/s

c) 200 m/s

d) 210 m/s

e) 240 m/s

Um gás ideal é levado de uma temperatura inicial Ti a uma temperatura final maior Tf ao longo de duas trajetórias reversíveis. A trajetória A é a pressão constante e a trajetória B é a volume constante. Qual é a relação entre as variações de entropia do gás para essas trajetórias?

a) ;

b) ;

c) ;

d) apenas se a temperatura inicial for baixa;

e) apenas se a temperatura inicial for elevada;

Se um gás ideal monoatômico com N moléculas está em equilíbrio térmico com um gás diatômico com o mesmo número de moléculas e o equilíbrio térmico é mantido quando a temperatura aumenta, a razão entre as variações da energia interna dos dois gases, / é:

a) 5/3;

b) 1;

c) 1/2;

d) 3/5;

e) 2;

Uma máquina de Carnot recebe 3.000 J na forma de calor de um reservatório térmico que está a uma temperatura = 500 K e rejeita calor para um reservatório térmico que está a uma temperatura = 325 K. Qual é a eficiência dessa máquina de Carnot?

a) 35%;

b) 25%;

c) 15%;

d) 20%;

e) 50%;

Um gás monoatômico ideal, a uma temperatura inicial (em K), se expande de um volume inicial para um volume 2 por cinco processos indicados no diagrama T-V da figura. O único processo que pode corresponder a uma expansão adiabática é:

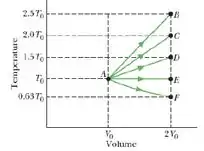
a) AF;

b) AB;

c) AC;

d) AD;

e) AE;

Um mol de um gás ideal diatômico, contido num recipiente munido de um pistão móvel, inicialmente a , se expande isotermicamente de um volume até que o seu volume triplique. A seguir sofre uma contração isobárica à pressão P até voltar ao seu volume inicial. Finalmente, o gás é aquecido isocoricamente até voltar à temperatura inicial.Considere que não ativa graus de liberdade vibracionais das moléculas do gás. Use .

a) Desenhe o diagrama PV associado, indicando todos os pontos relevantes. Deixe claro cada um dos processos descritos acima.

b) Calcule a temperatura T do gás ao final da compressão isobárica, em termos de e R, a constante dos gases ideais.

c) Calcule o trabalho total realizado pelo gás,em termos de e R.

d) Calcule o calor trocado durante o aquecimento isocórico,em termos de e R.

e) Calcule o rendimento deste ciclo.

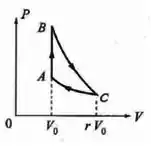
Numa máquina térmica, o agente é um mol degás ideal de coeficiente adiabático, que executa o ciclo da figura abaixo, onde BC é uma adiabática e CA uma isoterma.Definindo =,= e = , em termos de r, , , e :

a) Calcule PC;

b) Calcule PB;

c) Calcule TB;

d) Calcule o trabalho no processo BC;

e) Calcule a variação da entropia do gás no processo CA.

Observação: Qualquer resultado que não esteja fornecido no formulário em anexo deve ser DEMONSTRADO.