Numa máquina térmica, o agente é um mol degás ideal de coeficiente adiabático, que executa o ciclo da figura abaixo, onde BC é uma adiabática e CA uma isoterma.Definindo =,= e = , em termos de r, , , e :
a) Calcule PC;
b) Calcule PB;
c) Calcule TB;
d) Calcule o trabalho no processo BC;
e) Calcule a variação da entropia do gás no processo CA.
Observação: Qualquer resultado que não esteja fornecido no formulário em anexo deve ser DEMONSTRADO.
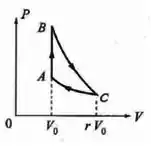
Passo 1
a) No processo podemos fazer:
Porque a temperatura é constante entre esses dois pontos!
Mas:
Então:
Passo 2
b) No processo podemos fazer:
E sabemos:
Trocando:
Passo 3
c) No processo podemos fazer:
E:
Então:
Passo 4
d) O processo é adiabático. Então:
Pela 1ᵃ Lei da Termodinâmica temos:
E:
Em que g é o número de graus de liberdade. Se acharmos achamos , show?
Presta atenção então no que eu vou fazer aqui.
Como ele não disse se é um gás monoatômico ou diatômico, não sabemos g. Mas sabemos , e podemos escrever g em função de :
Trocando o que a gente conhece então:
No ponto A:
Como n=1:
Vou trocar então por , só pra não ter R na resposta, como o enunciado pediu:
Show! Como o trabalho é :
Passo 5
e) Eiiii, vou te ensinar um macete. Sempre que a temperatura for constante ao longo do processo, você pode escrever:
Não precisa integrar!
O processo é isotérmico, a temperatura não varia, então podemos fazer:
A temperatura vai ser .
Como a temperatura não varia, a energia interna também não varia.
Então, pela 1ᵃ Lei da Termodinâmica, podemos escrever:
Show! Vamos achar o trabalho então que o problema tá resolvido.
Passo 6
O trabalho no processo vai ser:
Lembrando que n=1, e vou usar a mesma relação de antes:
Como:
E voltando na variação de entropia:
Lembrando que:
Resposta
a)
b)
c)
d)
e)