Um mol de um gás ideal diatômico, contido num recipiente munido de um pistão móvel, inicialmente a , se expande isotermicamente de um volume até que o seu volume triplique. A seguir sofre uma contração isobárica à pressão P até voltar ao seu volume inicial. Finalmente, o gás é aquecido isocoricamente até voltar à temperatura inicial.Considere que não ativa graus de liberdade vibracionais das moléculas do gás. Use .
a) Desenhe o diagrama PV associado, indicando todos os pontos relevantes. Deixe claro cada um dos processos descritos acima.
b) Calcule a temperatura T do gás ao final da compressão isobárica, em termos de e R, a constante dos gases ideais.
c) Calcule o trabalho total realizado pelo gás,em termos de e R.
d) Calcule o calor trocado durante o aquecimento isocórico,em termos de e R.
e) Calcule o rendimento deste ciclo.
Passo 1
a) Vou chamar os pontos no processo de 1, 2 e 3.
Como no processo o gás se expande isotermicamente, podemos escrever:
A pressão em 2 vai ser menor que em 1!
Beleza! No processo a pressão é constante, então:
E o enunciado disse pra gente que a pressão no ponto 3 é P! Então:
E como ele volta ao volume inicial:
N processo ele é aquecido isocoricamente até a temperatura inicial. Então esse processo vai ser uma reta vertical do ponto 3 até o ponto 1. E o gráfico vai ficar:
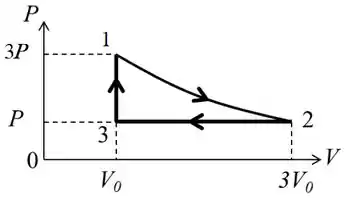
Passo 2
b) No processo como a pressão é constante, podemos escrever:
Passo 3
c) Vamos calcular o trabalho em todos os processo!
No processo :
No processo :
No processo :
Então:
O trabalho total no ciclo vai ser:
Vamos melhorar essa resposta?
No ponto 3:
Como n=1:
E trocando no trabalho:
Passo 4
d) O calor no processo vai ser a volume constante. Então:
Lembrando que:
E g, o número de graus de liberdade, vai ser igual a 5 porque é um gás diatômico! Então:
Passo 5
e) O rendimento vai ser:
O trabalho no ciclo nós já calculamos. Vamos calcular então o calor em todos os processos!
No processo :
Como é um processo isotérmico, não tem variação de energia interna. Então:
No processo :
Como a pressão é constante, vamos usar:
No processo :
Já calculamos, né?
Como é negativo:
O rendimento vai ser:
Resposta
a)
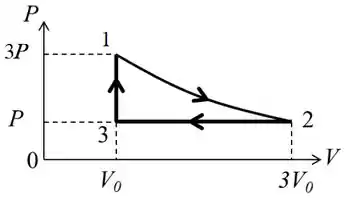
b)
c)
d)
e)