P3 de Física 3 - FIS1051 da PUCRIO - 2018.2

Um trilho condutor em forma de semicircunferência de raio está imerso numa região com campo magnético externo  de módulo (uniforme e constante), de direção perpendicular à página e com sentido saindo do papel. Um circuito elétrico de resistência total constante é completado por dois trilhos condutores retilíneos que partem do centro da circunferência: um horizontal, fixo, e outro móvel, que faz com o primeiro um ângulo variável [ , s].

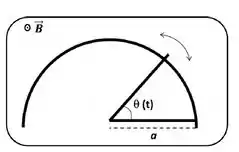
1. Calcule a induzida no circuito como função do tempo, . [Sugestão: Lembre que a área de um setor circular de raio e ângulo em radianos é dada por ] .
2. Calcule o instante em que a corrente induzida se anula. Nos intervalos e , qual é o sentido da corrente no circuito, horário ou anti-horário? (Justifique.)
3. Calcule o valor máximo que a corrente assume no intervalo .

Considere ainda a mesma função do enunciado principal, mas que agora o campo magnético externo varie no tempo em vez de ser constante.

4. Determine uma função para que a corrente induzida no circuito seja sempre nula.

No circuito da figura, tem-se , , , e . Inicialmente o capacitor está descarregado e o indutor está sem energia. No circuito, ocorrem as seguintes fases sucessivas:

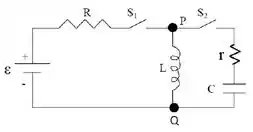
Fase 1: chave fechada e aberta durante longo tempo.

Fase 2: chave aberta e fechada durante longo tempo.

1. Encontre a expressão para a corrente no indutor em função do tempo durante a Fase 1.

Sabe-se que a carga no capacitor durante a Fase 2 tem a seguinte expressão geral (aqui o tempo é medido a partir do fechamento da chave ):

2. Determine o valor do coeficiente de amortecimento , da frequência angular e da fase .
3. Escreva a expressão geral para a corrente em função do tempo durante a Fase 2, usando os valores obtidos no item a), assim como os valores para a corrente inicial e para .
4. Desenhe o circuito sem a fonte, indicando o sentido da corrente inicial e as polaridades das tensões em todos os seus elementos. Em seguida, determine expressões para as tensões no resistor e no capacitor em função do tempo durante a Fase 2.

No circuito da figura, , e o capacitor é de um tipo variável, com uma capacitância ajustável de a . O circuito é conectado a um gerado com , onde .

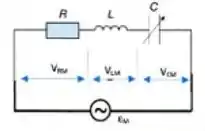
Nestas condições:

1. Calcule o valor que deve assumir para se ter um fator de potência igual a .
2. Calcule a amplitude da corrente.
3. Calcule as amplitudes das tensões , e .
4. Desenhe o diagrama de .

Para colocar o circuito em condição de ressonância, você deve mudar o valor do capacitor:

5. Calcule o novo valor de para obter a condição de ressonância do circuito e, nesta condição, calcule os valores da potência média dissipada em e da potência média fornecida ao circuito pelo gerador.