No circuito da figura, , e o capacitor é de um tipo variável, com uma capacitância ajustável de a . O circuito é conectado a um gerado com , onde .
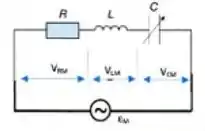
Nestas condições:
- Calcule o valor que deve assumir para se ter um fator de potência igual a .
- Calcule a amplitude da corrente.
- Calcule as amplitudes das tensões , e .
- Desenhe o diagrama de .
- Calcule o novo valor de para obter a condição de ressonância do circuito e, nesta condição, calcule os valores da potência média dissipada em e da potência média fornecida ao circuito pelo gerador.
Para colocar o circuito em condição de ressonância, você deve mudar o valor do capacitor:
Passo 1
a) Como , então . Agora, temos a seguinte relação para a tangente de
Como temos os valores para , e , podemos utilizar essa equação para obter
Passo 2
b) A amplitude da corrente é dada por
em que é a impedância e tem a seguinte expressão:
Dados os valores fornecidos no enunciado e o valor da capacitância que acabamos de encontrar, as impedâncias capacitiva e indutiva serão dados por
Substituindo em , obteremos
A amplitude da corrente será
Passo 3
c) No resistor, a amplitude de tensão será
No capacitor
No indutor
Passo 4
d) Para desenharmos os , precisamos nos lembrar que a corrente no resistor está em fase com a corrente; a corrente no capacitor está atrasada de e a corrente no indutor adiantada de .
Além disso, a corrente está atrasada de um ângulo igual a em relação à tensão . Por isso, teremos a seguinte representação:
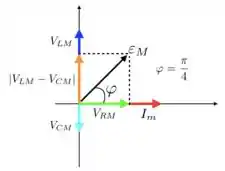
Passo 5
e) Para que o circuito entre em ressonância, temos que ter
ou seja, a impedância capacitiva é igual impedância indutiva.
Agora, como o problema já deu pra gente a frequência angular e o valor da indutância , então a nova capacitância será dada por
Na ressonância (), temos que a impedância é dada por
Por isso, para esse caso, temos que a amplitude da corrente no circuito será igual a
Passo 6
e) Continuação...
Com isso, conseguimos calcular o valor da potência média dissipada no resistor, que será
A potência fornecida média é dada por
Outra característica importante de um circuito em ressonância é que a fase , pois
Jogando essa fase em junto com os valores do enunciado, teremos
Portanto,