P3 de Física 3 - FIS1051 da PUCRIO - 2019.2

Em uma região do espaço existe um campo magnético de magnitude (onde ). Um aro condutor, de resistência constante , é descrito pela equação no plano

onde é uma constante com dimensão de tempo. Esse aro se expande com o tempo.

a) Calcule o fluxo magnético no aro como função do tempo.

b) Calcule a f.e.m. no aro e a corrente sobre o mesmo. Justifique se a corrente flui no sentido horário ou anti-horário quando a orientação positiva do aro é dada pelo vetor unitário (ou seja, o sentido positivo é o anti-horário).

c) Calcule a energia total dissipada no aro entre os instantes e .

No circuito RLC em série e sem fonte da Figura 1, , e . No instante , a corrente no circuito é , a carga no capacitor é e o capacitor está sendo carregado (isto é, a carga é positiva e aumenta).

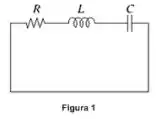
Inicialmente, suponha que o resistor não existe.

(a) Determine a carga máxima no capacitor.

(b) Determine a corrente máxima no circuito.

(c) Se a carga no capacitor é dada por , determine o ângulo de fase .

Em seguida, considere a existência do resistor.

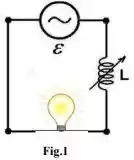
(d) Apresente, justificando, a nova expressão para . Em seguida, apresente um algoritmo (um procedimento detalhado, mas sem realizar as contas) para a determinação dos parâmetros e a partir dos dados do problema (, , , , ).

Um “dimmer” é um dispositivo que permite variar a intensidade luminosa de uma lâmpada. Estes dispositivos são compostos por uma bobina de indutância variável em série com uma lâmpada (Figura 1). A lâmpada é o elemento resistivo do circuito. O valor da indutância da bobina pode assumir qualquer valor entre e .

O circuito da Figura 1 é alimentado por um gerador alternado com uma f.e.m. eficaz e uma frequência angular . Considere que a potência média dissipada pela lâmpada não pode exceder e que a sua resistência elétrica é constante (não varia nem com a temperatura nem com outros fatores).

a) Calcule qual deve ser o valor mínimo da indutância no intervalo fornecido para que a potência média dissipada na lâmpada seja máxima . Calcule também o valor da resistência da lâmpada.

b) Calcule qual deve ser o valor da indutância para que a potência média dissipada pela lâmpada seja .

c) Se no lugar do gerador de f.e.m. alternada fosse inserida uma bateria de corrente continua , qual deveria ser o valor da tensão para que, decorrido um tempo muito longo, a potência dissipada na lâmpada fosse de ?

Considere novamente o circuito da Figura 1. Agora a lâmpada é substituída por um resistor e no circuito é inserido em série um capacitor .

d) (0,5) Considerando que a indutância possui o valor máximo calculado no item (b) desenhe o diagrama de fasores do circuito. A corrente que passa no circuito está adiantada ou atrasada em relação à tensão do gerador?

e) (1,0) Variando o valor da indutância L entre os limites permitidos, e , é possível fazer com que o circuito entre em ressonância? No caso de resposta negativa, justifique. No caso de resposta afirmativa, calcule o valor de para que isso aconteça.