P1 de Física 3 - FIS1051 da PUCRIO - 2020.1

Uma casca esférica de raio interno e raio externo possui uma densidade volumétrica de carga esfericamente simétrica que obedece à relação , onde é a distância entre o centro da esfera e o ponto de avaliação. Calcule o campo elétrico nas regiões:

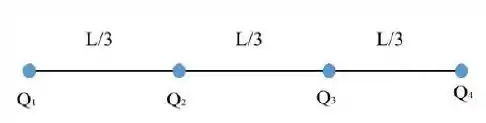
Quatro cargas e, estão fixadas em um segmento de reta de comprimento de reta, como mostra a figura.

1. Calcule a energia potencial eletrostática total para o sistema das quatro cargas.

Suponha que as cargas sejam, na realidade, partículas de massas idênticas . No instante , todas as partículas estão em repouso, na configuração mostrada na figura. Nesse instante, as partículas são soltas (todas com velocidades nulas) e passam a se mover apenas sob a ação das forças eletrostáticas.

2. Encontre e justifique o valor total da energia cinética para o sistema quando o tempo tende a infinito.

q = 5   n C ; e (b) uma esfera maciça isolante de raio, com carga total desconhecida, distribuída de maneira uniforme, conforme mostram as figuras. Ao traçarmos uma superfície Gaussiana fechada no formato de uma semiesfera de raio concêntrica com a esfera maciça, obtemos que o fluxo elétrico através dessa superfície é: . Encontre a densidade volumétrica de carga da esfera. (Nos cálculos, considere ).

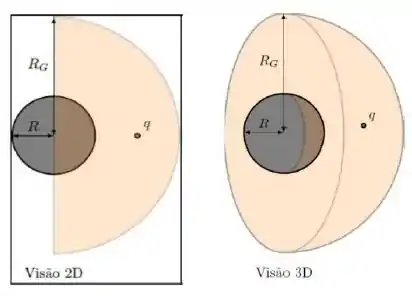
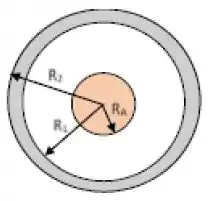
Uma casca esférica condutora de raio interno e raio externo é carregada com uma carga liquida positiva . No interior da casca é posicionada uma pequena esfera condutora, de raio , carregada com a mesma carga Considere que no infinito e que

1. Determine as expressões do potencial elétrico nas regiões:
2. Se uma carga igual a é transportada do infinito até ser depositada na casca esférica, calcule (utilizando os valores fornecidos), nesta nova condição, quais são as densidades de carga superficiais na superfície da esfera de raio e nas superfícies internas e externas da casca esférica.

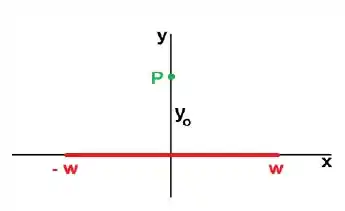
A fita cuja seção transversal está mostrada na Figura tem largura , espessura desprezível e comprimento infinito ao longo do eixo z. Está carregada com a densidade superficial de carga onde é constante e positiva .

1. Inicialmente, determine uma expressão geral para o vetor campo elétrico devido a um fio infinito carregado com uma densidade linear de carga positiva (), observando seu módulo e sentido em cada ponto do espaço.
2. Em seguida, considere que a fita pode ser decomposta em fios de espessuras infinitesimais. Finalmente, use o resultado do item anterior para determinar o vetor campo elétrico (módulo e sentido) devido à fita em um ponto de observação arbitrário do eixo situado acima dela e que dista da origem.

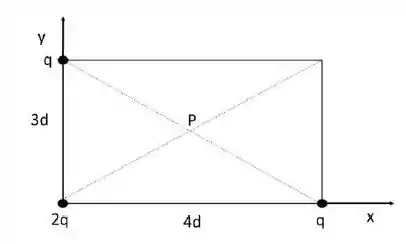
Três cargas, de valores estão colocadas nos vértices de um retângulo de lados e, como mostra a figura.

1. Expresse as forças eletrostáticas vetoriais agindo nas partículas localizadas em , e .
2. Uma partícula de carga é colocada na posição , que é o centro do retângulo. Calcule o módulo da força eletrostática devida ás três cargas sobre essa partícula.

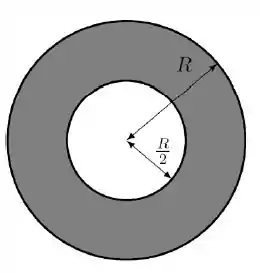
Uma coroa circular isolante, plana, com raio interno e raio externo ,possui uma quantidade total de carga . Esta carga é distribuída de maneira não uniforme sobre a coroa circular, de tal forma que a densidade superficial é dada por: , onde é uma constante positiva e é a distância do centro da coroa circular até qualquer ponto sobre ela, como mostrado na figura. Considere que o potencial é nulo no infinito ( no infinito).

1. Calcule a carga total na coroa circular em função de e dos raios e .
2. Calcule o potencial no centro da coroa circular, deixando a sua expressão em função de e dos outros dados do problema.

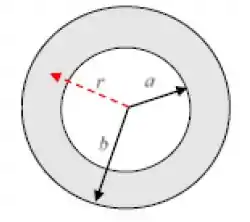
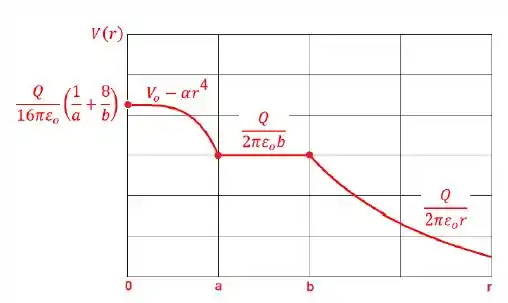
Um isolante esférico de raio a tem carga total Q (positiva) e está envolvido por uma casca esférica concêntrica de raios e , condutora em equilíbrio eletrostático. Não se sabe se a distribuição da carga no interior do isolante é uniforme ou não. A estrutura está imersa no vácuo (para O potencial elétrico em todos os pontos do espaço está caracterizado na Figura. Em particular, observam-se as dependências de V(r) com o raio r nos intervalos ; e que .

a) Após determinar o valor de  em função de Q, a, b e (considerando que o potencial é uma função contínua de , obtenha expressões para o campo elétrico em todos os pontos do espaço).

b) Em seguida, determine as distribuições superficiais de carga (com sinais) nas superfícies interna (raio ) e externa (raio b) da casca condutora. Calcule a carga líquida da casca condutora, se houver.