P1 de Física B - FIS1026 da PUCRIO - 2013.2

Um corpo de massa descreve um movimento acelerado em um plano e tem sua posição em função do tempo dada pelas equações: e . Usar o S.I.

Calcule e escreva em notação vetorial a velocidade do corpo no instante

Calcule e escreva em notação vetorial a força que atua no corpo no instante do item .

Um navio está ao norte e a leste do navio . O navio está navegando com uma velocidade constante de na direção sul; o navio navega com uma velocidade constante de em direção ao norte do leste.

Escreva uma expressão para o vetor posição de em relação à em função do tempo considerando o instante como o instante e que os navios estão nas posições iniciais descritas acima. (Sugestão: faça um desenho para orientá-lo na sua solução posicionando o navio na origem do sistema de coordenadas em ).

O plano abaixo tem inclinação em relação à horizontal igual a . Duas cordas inextensíveis e uma polia, ambas sem massa, mantém em equilíbrio três caixas. Despreze o atrito entre as caixas e o plano. Responda aos itens abaixo, sabendo que a caixa tem massa igual a , a caixa tem massa igual a , e que .

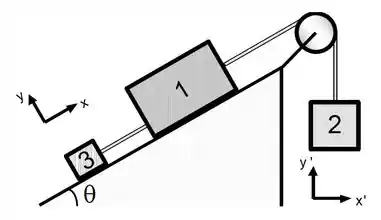
Escreva a expressão literal para as equações de movimento das três caixas, em termos das suas componentes, utilizando os respectivos sistemas de coordenadas indicados na figura. Em seguida calcule o valor da massa da caixa .

Calcule e escreva utilizando notação vetorial a força normal que a caixa exerce sobre o plano.

Suponha agora que a caixa tem massa igual a . Calcule a componente horizontal da aceleração da caixa .

Uma moeda de massa repousa sobre um bloco de massa . Ambos estão sobre uma plataforma circular de raio que gira com 60 rotaçoes por minuto em torno de um eixo na direção vertical. Os coeficientes de atrito estático e cinético entre o bloco e a plataforma são respectivamente e . O coeficiente de atrito estático e cinético entre a moeda e o bloco são respectivamente e . Use e .

Calcule as forças centrípetas que atuam na moeda e no bloco.

Faça um diagrama de corpo livre da moeda e do bloco e indique (se houver) os pares ação-reação.

Calcule a força de atrito que atua entre o bloco e a plataforma.

Qual é a máxima rotação por minuto que a plataforma pode ter antes que o bloco ou a moeda caiam da plataforma.