P2 de Física B - FIS1026 da PUCRIO - 2018.2

Um disco de massa e diâmetro e uma corda de massa desprezível e comprimento formam um pêndulo simples, que pode girar sem atrito em torno da origem do sistema de coordenadas ilustrado na figura. O pêndulo é largado do repouso a partir da horizontal. Quando o pêndulo está em sua posição mais baixa, como ilustrado em pontilhado na figura, ele colide com um bloco quadrado de lado e mesma massa, que está em repouso sobre uma superfície horizontal áspera. O coeficiente de atrito cinético entre o bloco e a superfície vale . A colisão ocorre durante o intervalo de tempo de um centésimo de segundo.

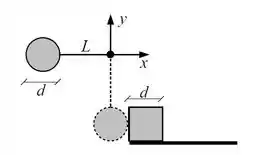
a) Calcule a posição do centro de massa do sistema (disco e bloco) imediatamente antes da colisão.

b) Sabendo que o pêndulo fica parado imediatamente após a colisão, calcule a velocidade do bloco para este instante de tempo.

c)Calcule a força média que o bloco faz no pêndulo durante a colisão.

d) Calcule distância percorrida pelo bloco até parar.

Uma partícula em repouso está sobre uma mesa horizontal com atrito desprezível e cujo centro de massa coincide com a origem de coordenadas . No instante ela explode em três partículas menores. A partícula 1 se afasta da origem de coordenadas com um momento linear . A partícula 2 se afasta da origem com um momento linear .

a) Determine o momento linear da partícula 3 e o ângulo que ele faz em relação ao eixo 𝑥 positivo.

b) Sabendo que a explosão dura , calcule as forças responsáveis pela explosão e mostre que durante este processo .

c) Calcule a posição do centro de massa do sistema após a explosão.

Um objeto composto por uma haste muito fina de massa e comprimento e um aro fino de raio e massa é livre para girar em torno dos eixos e. A origem do eixo de coordenadas está no centro do aro e no centro da haste. Nos cálculos utilize 3 números significativos.

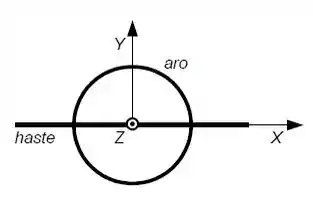
a) Calcule o momento de inércia do objeto em torno dos eixos e . Em torno de qual eixo é mais fácil girar o objeto?

b) O objeto do item anterior é acelerado em torno do eixo . Partindo do repouso, no tempo ele alcança uma velocidade angular . Determine neste instante de tempo quais são os módulos das acelerações tangencial e radial na extremidade da haste.