P3 de Física B - FIS1026 da PUCRIO - 2012.1

Um aro uniforme de raio e massa está preso a um fio de massa desprezível e está girando em uma superfície horizontal. Na figura abaixo, a trajetória do centro de massa do aro está indicada pela circunferência tracejada. A trajetória tem raio e a velocidade angular do aro é . Suponha inicialmente que não há atrito entre o aro e a superfície.

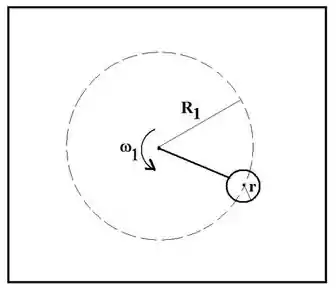
Escreva o módulo do momento angular do aro em relação ao centro da trajetória.

Um dispositivo oculto no centro da trajetória diminui o raio para . Neste novo raio, qual é o novo valor da velocidade angular ? Justifique claramente o conceito

físico utilizado.

Encontre o trabalho realizado pelo dispositivo oculto da letra b.

Suponha agora que há atrito entre o aro e a superfície. Se no instante o aro está girando na circunferência de raio (original) e com velocidade angular , e que o coeficiente de atrito estático é e o de atrito cinético é , calcule o intervalo de tempo que o aro demora em parar totalmente.

Considere o sistema abaixo, onde um cilindro maciço de massa e raio pode girar sem atrito em torno de um eixo vertical fixo à superfície, que passa pelo seu centro de massa. Uma corda ideal e de massa desprezível está enrolada em torno do cilindro, passa por uma polia em forma de aro com massa e raio e está presa a um bloco de massa desconhecida. Não há atrito nos eixos da rotação da polia e do cilindro e não ocorre escorregamento da corda no cilindro ou na polia. Tampouco há atrito entre o bloco e a superfície do plano inclinado. O raio da polia (aro) vale e o ângulo é . Observa-se que o bloco desce com uma aceleração linear .

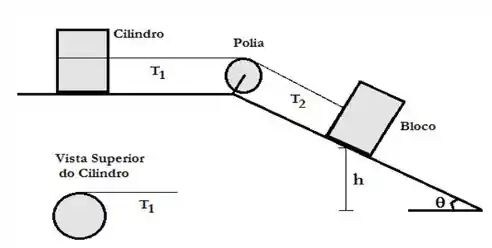
Havendo o sistema partido do repouso, observa-se que a polia sofre um deslocamento angular total de radianos até que o bloco chegue à base da rampa. Determine o tempo de queda do bloco, , e a velocidade angular final do cilindro maciço, .

Faça o diagrama do corpo livre para cada componente do sistema, representando claramente as forças que agem em cada um dos componentes e o sentido de seus movimentos (de translação ou rotação).

Escreva as equações resultantes das Leis de Newton (rotacional e translacional) para

os três corpos.

A partir das equações da letra , determine o valor da massa do bloco, em termos

de .

Um disco de raio e massa desce sem deslizar, a partir do repouso, a rampa inclinada conforme a figura. Após chegar à base da rampa , ele segue na horizontal para a pista em forma de circunferência com raio e sobe essa pista rolando sem deslizar. O ângulo entre a rampa e a horizontal é . O raio do disco vale e o comprimento da rampa, do ponto ao ponto , vale , onde é o raio da pista circular. A aceleração da gravidade local é . A linha tracejada corresponde a uma possível trajetória do centro de massa do disco.

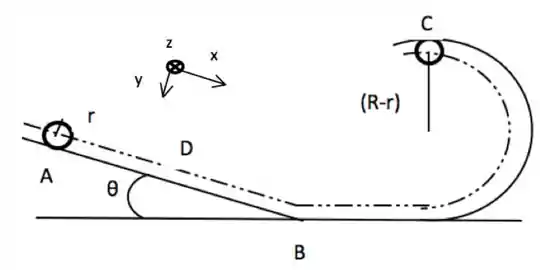
Faça o diagrama de forças para o disco durante o percurso de até . A partir das leis sobre torque e força, obtenha uma expressão literal, em função de , para o valor da aceleração do do disco entre e . Use o sistema de coordenadas desenhado na

figura.

Indique claramente o sentido da força de atrito estática feita pela superfície da rampa sobre o disco. Determine uma expressão literal para , em função de e . Resolva através da segunda lei de Newton aplicada ao centro de massa do disco.

Encontre uma expressão literal para o valor da velocidade angular do disco em

torno de um eixo horizontal que passe em seu , quando o disco chega ao ponto , em

função de e . Resolva através do uso de leis físicas referentes à energia mecânica.

O valor mínimo da velocidade do do disco para passar no ponto mais alto da

pista circular , sem perder o contato com a pista, é .

Obtenha uma expressão literal para a velocidade do do disco no ponto , , em

função de e através de leis físicas sobre a energia mecânica. Compare com o valor

mínimo dado e diga se o disco passará pelo ponto em contato com a pista ou se descolará dela antes de chegar a .