P2 de Física B - FIS1026 da PUCRIO - 2015.1

Em um bate-estaca, o martelo com massa é elevado até uma altura acima do topo de uma viga vertical que deve ser cravada no solo. Cada vez que o martelo é solto e colide com a viga e ela desce para dentro do solo. O martelo é guiado por trilhos verticais que produzem nele uma força de atrito constante de módulo igual a . Utilize considerações de trabalho e energia para responder as perguntas abaixo.

a) Calcule os trabalhos realizados pela força da gravidade e pela força de atrito sobre o martelo, desde quando ele é solto até o instante em que ele atinge a viga. Considere o eixo positivo apontando para cima.

b) Calcule o módulo da velocidade com que o martelo atinge a viga.

c) Considere que a colisão entre o martelo e a viga é completamente inelástica e que a massa da viga é igual a . Calcule a força média resultante que age sobre o sistema martelo-viga enquanto a viga está sendo cravada.

d) Calcule o percentual de energia dissipada em relação à energia inicial durante a colisão.

Um corpo de massa parte do repouso no ponto , situado a uma altura sobre uma rampa curva e com atrito desprezível. Admita a energia potencial gravitacional como sendo nula em . O corpo chega ao final da rampa em com velocidade , onde se inicia um trecho horizontal com comprimento . Neste trecho , o coeficiente de atrito cinético entre o corpo e a superfície cresce linearmente com a posição , tal que . Após o ponto o corpo choca-se com uma mola ideal de constante elástica e a comprime uma distância até parar. Durante a compressão da mola, o coeficiente de atrito cinético entre o corpo e a superfície é constante e vale . Utilize considerações de trabalho e energia para responder as perguntas abaixo.

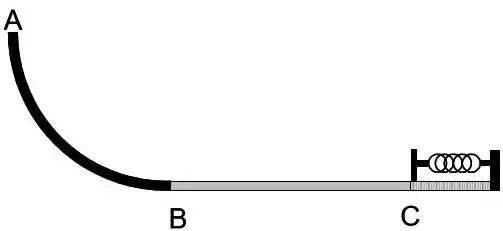
a) Calcule o valor da energia potencial gravitacional do corpo em .

b) Esboce o gráfico do módulo da força de atrito cinético versus a distância percorrida pelo corpo no trecho e calcule o módulo da velocidade que o corpo possui ao atingir a mola em .

c) Usando o Teorema do trabalho-energia cinética, calcule a compressão sofrida pela mola em centímetros.

Em um dos últimos jogos olímpicos de inverno, a final de Curling foi disputada entre Canadá e Rússia. O jogo consiste em posicionar pedras dentro de um alvo. Em uma de suas jogadas a equipe canadense realizou uma proeza típica de uma equipe vencedora. A figura abaixo representa a pista de gelo vista de cima. As duas pedras e da equipe russa estão em repouso e foram posicionadas durante o jogo. Uma terceira pedra a ser lançada pela equipe canadense está também ilustrada. A pedra lançada com velocidade , consegue acertar a pedra russa em uma colisão elástica bidimensional expelindo para fora do alvo com uma velocidade de módulo , sua trajetória faz um ângulo com a horizontal. Na sequencia a pedra faz uma segunda colisão elástica unidimensional com a pedra expelindo-a para fora do alvo. Considere todo atrito entre as pedras e o solo eliminado pelos outros membros das equipes com suas vassouras. Considere as massas de todas as pedras .

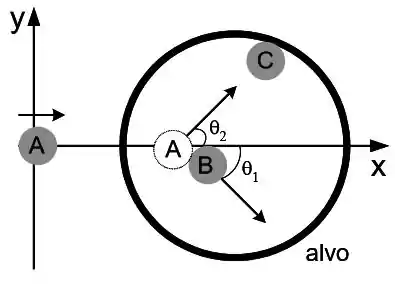
a) Determine a velocidade do centro de massa antes da primeira colisão.

b) Encontre o ângulo e a velocidade da pedra ao final da primeira colisão com a pedra .

c) Calcule a força média exercida pela pedra sobre a pedra durante a colisão que durou .

d) Considere agora a colisão entre as pedras e . Encontre e ao final da segunda colisão.