P2 de Física B - FIS1026 da PUCRIO - 2016.2

Seja a colisão entre uma esfera de massa , cujo vetor posição é dado por e outra esfera de massa e vetor posição é dado por Imediatamente após a colisão, a esfera adquire uma velocidade de módulo e faz um ângulo de em relação ao eixo positivo. Considere o sistema isolado. Justifique suas respostas.

(a) Dado que o momento total do sistema imediatamente antes da colisão é , determine a velocidade do centro de massa imediatamente após a colisão.

(b) Determine a velocidade da esfera A imediatamente após a colisão.

(c) Determine se a colisão foi elástica ou inelástica.

Um bate-estaca de gravidade funciona com um princípio muito simples. Um martelo de massa é solto do repouso a uma altura acima de uma estaca de massa . A colisão dura um intervalo de tempo muito curto . Imediatamente após a colisão o martelo e a estaca adquirem a mesma velocidade e chegam ao repouso, depois de afundarem uma distância . Suponha o intervalo de tempo de afundamento como sendo . Todo movimento acontece ao longo da direção vertical. Utilize o sistema de coordenadas abaixo, dê suas respostas em função dos dados do problema e dos vetores unitários e . Utilize para o módulo da aceleração da gravidade.

(b) Determine o impulso resultante na estaca durante a colisão.

Um bate-estaca de gravidade funciona com um princípio muito simples. Um martelo de massa é solto do repouso a uma altura acima de uma estaca de massa . A colisão dura um intervalo de tempo muito curto . Imediatamente após a colisão o martelo e a estaca adquirem a mesma velocidade e chegam ao repouso, depois de afundarem uma distância . Suponha o intervalo de tempo de afundamento como sendo . Todo movimento acontece ao longo da direção vertical. Utilize o sistema de coordenadas abaixo, dê suas respostas em função dos dados do problema e dos vetores unitários e . Utilize para o módulo da aceleração da gravidade.

(a) Determine qual é a velocidade com que o martelo chega na estaca.

Um bate-estaca de gravidade funciona com um princípio muito simples. Um martelo de massa é solto do repouso a uma altura acima de uma estaca de massa . A colisão dura um intervalo de tempo muito curto . Imediatamente após a colisão o martelo e a estaca adquirem a mesma velocidade e chegam ao repouso, depois de afundarem uma distância . Suponha o intervalo de tempo de afundamento como sendo . Todo movimento acontece ao longo da direção vertical. Utilize o sistema de coordenadas abaixo, dê suas respostas em função dos dados do problema e dos vetores unitários e . Utilize para o módulo da aceleração da gravidade.

(c) Considere agora os seguintes dados numéricos: , , , e . Calcule qual é a força média que o solo faz no sistema martelo-estaca durante o afundamento. Dê sua resposta utilizando o

Um toca-discos com um prato de diâmetro é posto em rotação por meio de uma correia ligada ao eixo de um motor de diâmetro . Veja a ilustração abaixo. Partindo do repouso, o prato alcança a velocidade angular final (rotações por minuto) em um intervalo de tempo Considere a correia como sendo inextensível e suponha as acelerações constantes. Resolva o problema literalmente para só no final substituir os valores numéricos.

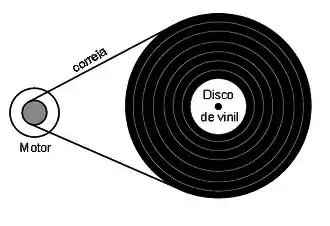
(a) Determine as acelerações angulares do motor e do prato do toca-discos.

(b) Determine quantas rotações o prato faz até atingir sua velocidade final.

(c) Determine os módulos das acelerações radial ar e tangencial at de um ponto na borda do prato após ele atingir a velocidade final.